Shack-Hartmann sensing with arbitrarily shaped pupil

Abstract

The measurements of Shack-Hartmann wavefront sensors in adaptive microscopy can be affected by missing or ill-formed spots behind the subapertures. This may change dynamically during operation, so an updatable control method is required. We provide a protocol along with Python code to update the wavefront corrector control matrix and command vector while performing Shack-Hartmann sensing with an arbitrarily shaped pupil for both zonal and modal control methods.

Introduction

When using adaptive microscopy to image thick biological specimens, strong scattering and aberrations can severely distort the pupil shape such that some Shack-Hartmann (SH) spots are unmeasurable within the subapertures during wavefront sensing. To accommodate for the loss of effective wavefront information, the wavefront corrector control matrix and command vector should be updated accordingly.

There are two types of wavefront control methods for SH-based adaptive optics, the zonal and the modal methods. The zonal method controls the wavefront corrector using raw slope data, while the modal method first converts the raw slope data to modal coefficients before using this information to control the corrector. The control matrix is updated differently for the two wavefront control methods and are both presented in this protocol. For simplicity, we will use a deformable mirror (DM) as the corrector device.

This document provides a brief introduction to the method presented in detail in Ref. [1] and its implementation in Python. The accompanying python code can be obtained from https://github.com/dop-oxford. Relevant Labview code is also available.

1. Zonal Control

Assume \(\text{S}\) is a slope vector measured by the Shack-Hartmann wavefront sensor (SHWS) that includes \(2M\) elements, where \(M\) is the number of subapertures of the SHWS. \(\text{R}_{\text{s}}\) is the DM slope response matrix and \(\text{A}\) is the DM command vector. For regular wavefront control, the DM slope control matrix can be obtained by performing singular value decomposition (SVD) of \(\text{R}_{\text{s}}\) and taking its pseudoinverse, resulting in \(\text{R}_{\text{s}}^{+}\). Then \(\text{A}\) can be calculated as

\[ \text{A} = \text{R}_{\text{s}}^{+}\text{S}\]

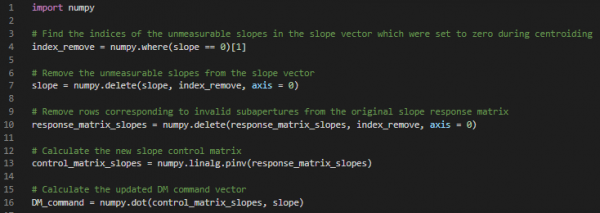
However, when the pupil is severely distorted, some SH spots may become too dim and dispersed to measure. In this case, instead of replacing the unmeasurable slopes in vector \(\text{S}\) with zero and using the original slope control matrix \(\text{R}_{\text{s}}^{+}\) [2], a more accurate method would be to first remove the unmeasurable slopes in vector \(\text{S}\) to obtain \(\widetilde{\text{S}}\) [1]. Then remove rows corresponding to invalid subapertures from \(\text{R}_{\text{s}}\) and recalculate its pseudoinverse \({\widetilde{\text{R}}}_{\text{s}}^{+}\). The updated DM command vector can therefore be calculated as

\[ \text{A}\text{=}{\widetilde{\text{R}}}_{\text{s}}^{+}\widetilde{\text{S}}\]

Python code for the above slope control matrix updating process is given below:

2. Modal Control

To perform wavefront correction over a circular pupil using modal control, the wavefront aberration can be decomposed into orthogonal modes defined over the pupil area commonly known as Zernike polynomials \(\left\{ Z \right\}\). Let \(K\) denote the number of Zernike polynomials used to reconstruct the wavefront, then the modal response matrix \(\text{R}_{\text{c}}\) and modal coefficient vector \(\text{B}\) can be converted from the slope response matrix \(\text{R}_{\text{s}}\) and slope vector \(\text{S}\) respectively, by using the following equations:

\[ \text{R}_{\text{c}}\text{=C}\text{R}_{\text{s}}\]

\[ \text{B}\text{=}\text{CS}\]

where \(\text{C}\) is a \(K \times 2M\) conversion matrix calculated as the pseudoinverse of the gradient of the Zernike polynomials, given by:

\[ \text{C=}\left( \nabla\text{Z} \right)^{\mathbf{+}}\]

However, for arbitrary pupils detected by the SHWS, Zernike polynomials lose orthogonality, and a new set of orthogonal modes need to be established, which we define as \(\left\{ Q \right\}\). \(\left\{ Q \right\}\) can be expressed as a linear combination of \(\left\{ Z \right\}\):

\[ Q_{l} = \sum_{k = 1}^{K}{\text{D}_{lk}Z_{k}}\]

where \(\text{D}_{lk}\) is a conversion coefficient between the \(k\text{th}\) Zernike polynomial and the \(l\text{th}\) new orthogonal mode. Let \(N\) denote the number of actuators of the DM, then the above equation can be given in matrix form as:

\[ \text{Q}\text{=}\text{Z}\text{D}^{\text{T}}\]

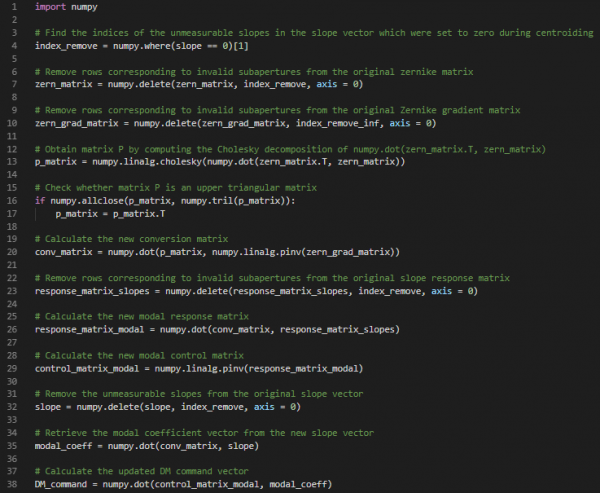
where \(\text{Q}\) is an \(M \times N\) matrix, \(\text{Z}\) is an\(\ M \times K\) matrix and \(\text{D}\) is an \(N \times K\) matrix. \(\text{Z}\) is evaluated at the central positions of the \(M\) subapertures and \(\text{Z}^{\text{T}}\text{Z}\) is a symmetric positive-definite matrix. Let \(\text{D}\text{=}\left( \text{P}^{\text{T}} \right)^{- 1}\), then \(\text{P}\) can be obtained uniquely by computing the Cholesky decomposition of \(\text{Z}^{\text{T}}\text{Z}\) [3]. \(\text{P}\) is an upper triangular matrix and \(\text{D}\) is a lower triangular matrix.

The following equations are then valid for an arbitrary pupil:

\[ {\widetilde{\text{R}}}_{\text{c}}\text{=}\text{P}\left( \nabla\widetilde{\text{Z}} \right)^{\mathbf{+}}{\widetilde{\text{R}}}_{\text{s}}\]

\[ \widetilde{\text{B}}\text{=}\text{P}\left( \nabla\widetilde{\text{Z}} \right)^{\mathbf{+}}\widetilde{\text{S}}\]

\[ \text{A=}{{\widetilde{\text{R}}}_{\text{c}}}^{\mathbf{+}}\widetilde{\text{B}}\]

where \({\widetilde{\text{R}}}_{\text{s}}\), \(\nabla\widetilde{\text{Z}}\) and \(\widetilde{\text{S}}\) are calculated from valid subapertures. As the pupil shape varies, matrix \(\text{P}\) should always be updated by the Cholesky decomposition of \({\widetilde{\text{Z}}}^{\text{T}}\widetilde{\text{Z}}\).

Python code for the above modal control matrix updating process is given below:

[1] Dong, B. and M.J. Booth, "Wavefront control in adaptive microscopy using Shack-Hartmann sensors with arbitrarily shaped pupils." Optics Express, 26(2): p. 1655-1669 (2018). 10.1364/OE.26.001655

[2] Rahman, S.A. and M.J. Booth, "Direct wavefront sensing in adaptive optical microscopy using backscattered light." Applied Optics, 52(22): p. 5523-5532 (2013). 10.1364/AO.52.005523

[3] Ye, J., et al., "Modal wavefront estimation from its slopes by numerical orthogonal transformation method over general shaped aperture." Optics Express, 23(20): p. 26208-26220 (2015). 10.1364/OE.23.026208