Microscope Resolution Estimation and Normalised Coordinates

1. Introduction

This note explains the context and derivations of normalised coordinates and “rules of thumb" frequently used in the estimation of resolution of microscopes. We do not attempt to provide a fully referenced review of this theory, but simply to present the main points. In any case, many of the rules used here are so widespread that they have the status of folklore. We hope that by summarising the derivations in one document, we can clarify the origin of these expressions.

2. Lateral resolution

Consider a system using a circular, thin, positive lens focussing monochromatic light of wavelength \(\lambda\) into a medium of refractive index \(n\). The lens has numerical aperture \(NA = n\mathrm{\sin}\alpha\), where \(\alpha\) is the maximum focussing angle. Derivations via scalar Fraunhofer diffraction theory lead to expressions for the focal intensity in the lateral plane, such as the integral equation representing integration over a circular pupil:

\[ \begin{equation} I(\rho,\xi) = \left| \int_{r = 0}^{1}{\int_{\theta = 0}^{2\pi}P}(r,\theta)\mathrm{\exp}\left\lbrack i\frac{2\pi n}{\lambda}\text{rρ}\mathrm{\cos}\left( \theta - \xi \right) \right\rbrack rdrd\theta \right|^{2} \end{equation}\]

where \((r,\theta)\) are the polar coordinates in the pupil (with normalised radius of 1), \((\rho,\xi)\) are the polar coordinates in the focal region and \(P(r,\theta)\) is the complex pupil function. Multiplying factors have been omitted, as they do not affect the shape of the focal intensity, which will be important for the following derivations. Evaluation of the integral for the case when \(P(r,\theta) = 1\) leads to the exact solution

\[ \begin{equation} I(v) = A\left| \frac{2J_{1}(v)}{v} \right|^{2} \end{equation}\]

where \(J_{1}\) is a Bessel function, \(A\) is a constant, and where we have introduced a normalised coordinate

\[ \begin{equation} v = \frac{2\pi NA\rho}{\lambda} = \frac{2\pi n\mathrm{\sin}\text{αρ}}{\lambda} \end{equation}\]

The normalised coordinate simplifies the expression of the focal intensity into a version that simply scales in size with the numerical aperture or inversely with the wavelength. Often treatments of this problem concerning only low NA provide a similar expression as

\[ \begin{equation} v = \frac{2\pi\rho}{\lambda}.\frac{a}{f} \end{equation}\]

where \(a\) is the radius of the lens and \(f\) is the focal length. \(n = 1\) is usually assumed for these cases.

We can use Eq. 2 to derive an approximation for the size of the focal spot. The first zero of the Bessel function \(J_{1}(t)\) occurs at \(t \approx 3.83\), which corresponds to \(\rho \approx 0.61\lambda/NA\). It follows that the diameter of the focal spot, defined as the diameter of the first zero in the Airy pattern, is given by

\[ \begin{equation} \Delta\rho_{0} = \frac{1.22\lambda}{\text{NA}} \end{equation}\]

The distance between the half maximum points of the intensity distribution (the full width half maximum, FWHM) is approximately half of the above value. Using an empirically determined scaling factor, obtained by fits to calculated values, the FHWM is given by

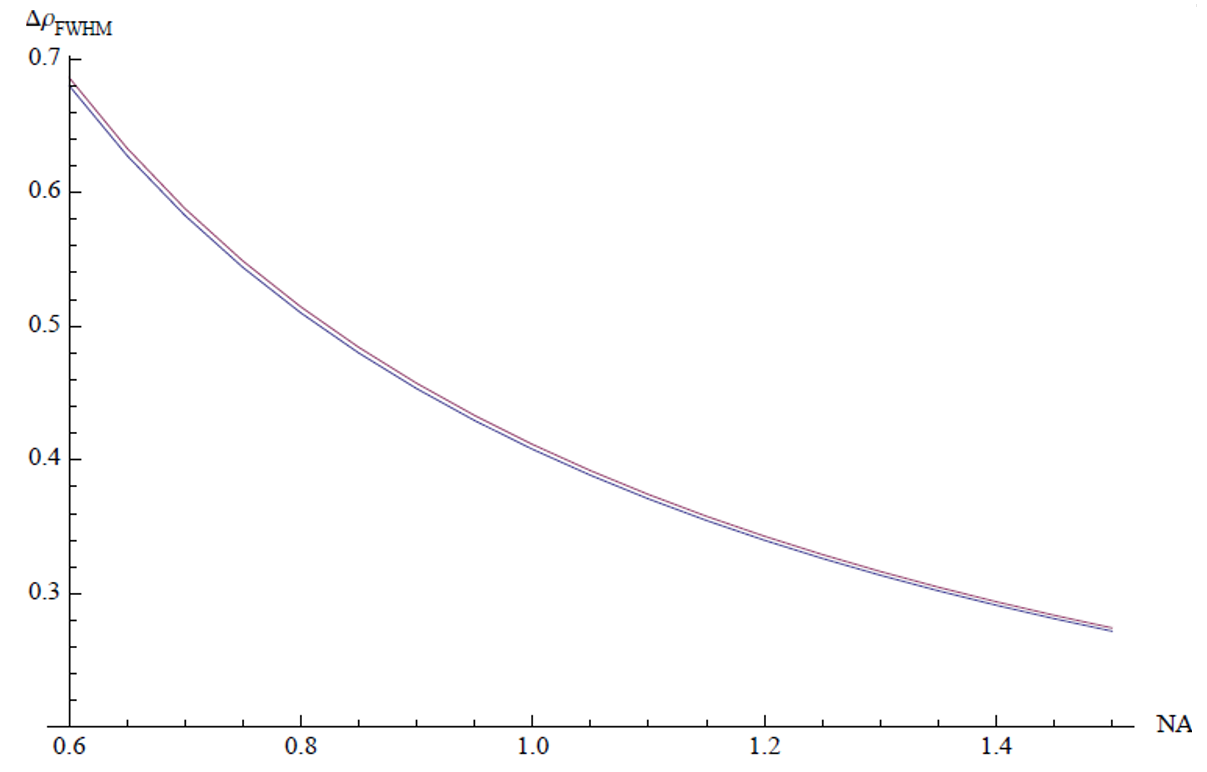
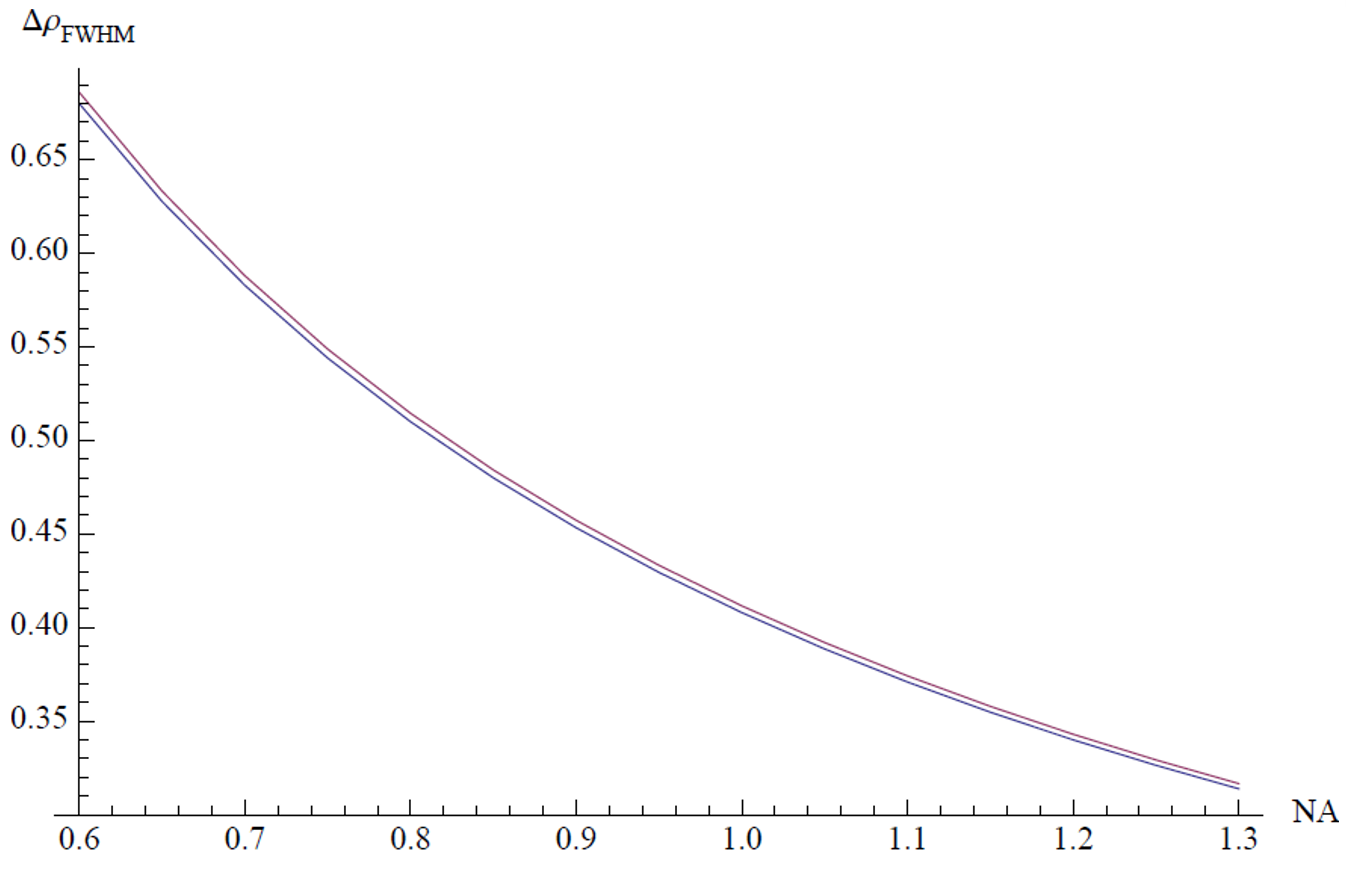
\[ \begin{equation} \Delta\rho_{\text{FWHM}} = \frac{0.51\lambda}{\text{NA}} \end{equation}\]

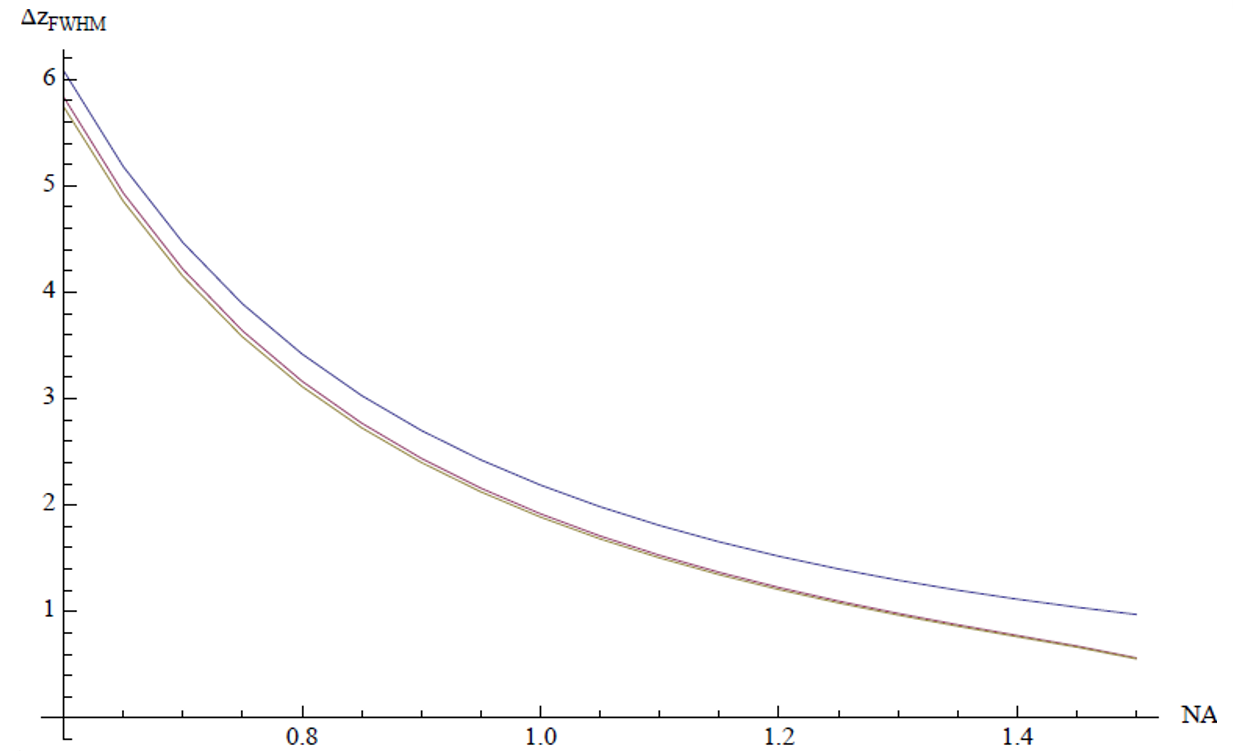
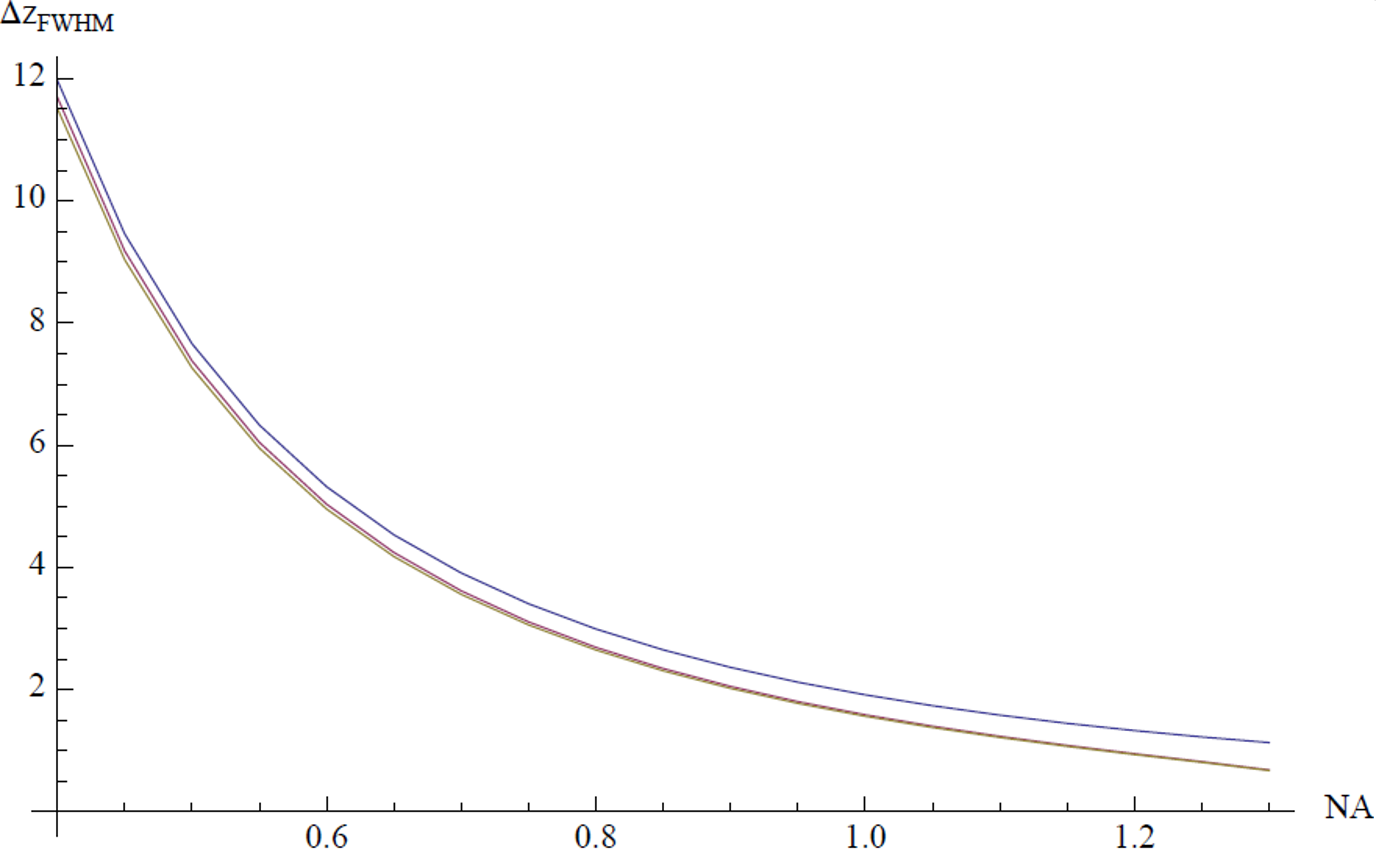
Figure 1 shows the calculated values of the axial FWHM using scalar diffraction theory and the approximation for an oil immersion lens. The corresponding calculation for a water immersion lens is shown in Figure 2.

3. Axial resolution

Diffraction calculations lead to the following expression for the variation of intensity along the optical axis:

\[ \begin{equation} I(u) = \left| \int_{r = 0}^{1}{\int_{\theta = 0}^{2\pi}P}(r,\theta)\mathrm{\exp}\left( i\frac{ur^{2}}{2} \right)rdrd\theta \right|^{2} \end{equation}\]

or, assuming \(P(r,\theta) = 1\), the exact solution

\[ \begin{equation} I(u) = C\left| \frac{\mathrm{\sin}(u/4)}{u/4} \right|^{2} \end{equation}\]

where \(C\) is a constant and the normalised coordinate \(u\) is defined as

\[ \begin{equation} u = \frac{8\pi nz}{\lambda}\mathrm{\sin}^{2}\left( \frac{\alpha}{2} \right) \end{equation}\]

In other derivations for the low NA case, this normalised axial coordinate is defined as

\[ \begin{equation} u = \frac{2\pi nz}{\lambda}\frac{a^{2}}{f^{2}} = \frac{2\pi z}{\lambda}.\frac{NA^{2}}{n} \end{equation}\]

Using small angle approximations to the sine functions, we see that \(NA = n\mathrm{\sin}\alpha \approx n\alpha\) and that \(\mathrm{\sin}^{2}(\alpha/2) \approx \alpha^{2}/4\) and thus that the definitions of Eqs. 9 and 10 are equivalent for low numerical aperture. They are not equivalent for higher numerical aperture systems.

Eq. 8 can be used to calculate the axial extent of the focus. The intensity is zero when \(u/4 = \pm \pi\) and hence when

\[ \begin{equation} z = \pm \frac{\lambda}{2n\mathrm{\sin}^{2}(\alpha/2)} \end{equation}\]

The distance along the axis between the zeros is therefore

\[ \begin{equation} \Delta z_{0} = \frac{\lambda}{n\mathrm{\sin}^{2}(\alpha/2)} \end{equation}\]

For low NA, we use \(\mathrm{\sin}^{2}(\alpha/2) \approx \alpha^{2}/4 \approx NA^{2}/4n^{2}\) to obtain

\[ \begin{equation} \Delta z_{0} = \frac{4n\lambda}{NA^{2}} \end{equation}\]

The distance between the half maximum points of the intensity distribution (the FWHM) is approximately half of the above value. Using an empirically determined scaling factor, obtained by fits to calculated values, the FHWM is given by

\[ \begin{equation} \Delta z_{\text{FWHM}} \approx \frac{0.45\lambda}{n\mathrm{\sin}^{2}(\alpha/2)} \approx \frac{1.8n\lambda}{NA^{2}} \end{equation}\]

where the last approximate expression is valid for low NA. An accurate expression can be obtained in terms of the NA via the trigonometric relationships

\[ \begin{equation} \mathrm{\sin}^{2}\left( \frac{\alpha}{2} \right) = \frac{1}{2}\left( 1 - \mathrm{\cos}\alpha \right) = \frac{1}{2}\left( 1 - \sqrt{1 - \mathrm{\sin}\alpha} \right) \end{equation}\]

into which we substitute \(\mathrm{\sin}\alpha = NA/n\) to obtain

\[ \begin{equation} \mathrm{\sin}^{2}\left( \frac{\alpha}{2} \right) = \frac{1}{2}\left( 1 - \sqrt{1 - \frac{NA^{2}}{n^{2}}} \right) \end{equation}\]

so that

\[ \begin{equation} \Delta z_{0} = \frac{2\lambda}{\left( n - \sqrt{n^{2} - NA^{2}} \right)} \end{equation}\]

and

\[ \begin{equation} \Delta z_{\text{FWHM}} = \frac{0.9\lambda}{\left( n - \sqrt{n^{2} - NA^{2}} \right)} \end{equation}\]

Figure 3 shows the calculated values of the axial FWHM using scalar diffraction theory and the two approximations for an oil immersion lens. The corresponding calculation for a water immersion lens is shown in Figure 4.