Practical implementation of adaptive optical microscopes

1. Introduction

There is a well-developed literature covering experimental results in adaptive optics (AO) for microscopy. However, by the nature of publications in scientific journals, the articles concentrate on conceptual advances and methods sections typically provide an overview, rather than detailed step-by-step guides to the design and implementation. In some cases, detailed designs are presented in supplementary documents, but these do not necessarily cover the reasoning for design decisions that were made during the development process. Such information covering design philosophy and issues of practical implementation is invaluable to those seeking to implement AO technology.

We aim in this guide to provide guidelines that will help in the design and implementation of AO systems for microscopes. Rather than present a specific guide for a particular system, we explain concepts and methods that are generally useful in these applications. This includes, for example, the reasons why particular design decisions are made in the optical systems that incorporate adaptive elements and practical tips for the set-up of such devices.

2. System design considerations

2.1 Limiting apertures

The AO microscope system should be designed around a chosen limiting aperture. For optimum performance (in terms of image resolution and signal level) this limit should usually be the pupil aperture in the objective lens. If an aperture placed elsewhere in the system has a smaller size when imaged onto the objective pupil, then the numerical aperture of the lens will be reduced. For this reason, it is important to make sure that the aperture of the adaptive element is imaged appropriately onto the objective pupil.

Dependent upon the design of the adaptive element (AE), whether a deformable mirror (DM) or a spatial light modulator (SLM), an aperture may be included in front of the active area. In most cases, though, the user is free to define the active area that will be used in the system. When using a SLM it is possible to define the aperture using diffractive patterns [1]; with a DM, the pupil is defined by an aperture at another plane in the system.

The system design should include as much of the active area as possible, in order to make sure that as many of the (expensive) actuators or pixels are usable. The best configuration is therefore to match the active pupil of the AE to the limiting aperture in the objective pupil. In order to achieve this, the magnification must be chosen correctly between the AE and the objective. Note however the comments in the later section of this document on “Deformable mirror active apertures”.

The radius a of the objective pupil can be calculated as

\[ a=F \times \textit{NA}=\frac{f \times \textit{NA}}{M} \]

where NA is the numerical aperture of the objective lens and M is the magnification, according to the lens specifications. F is the focal length of the objective lens, which may or may not be provided. Alternatively, the focal length f of the manufacturer’s tube lens can be used. For more information see reference [2].

2.2 Using different objective lenses

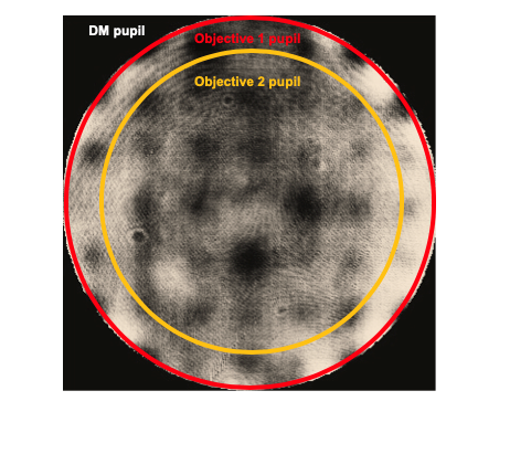
It should be remembered that different objective lenses have different pupil diameters. This presents problems for an AO microscope that uses multiple objectives, as it is not possible to match the AE and lens apertures with a fixed magnification relay and variable magnification is usually impractical. In this case, it is necessary to design the system so that the full AE aperture is used for the objective lens with the largest pupil. For the other lenses, the AE would in effect be underfilled and fewer actuators/pixels would be effectively utilised as shown in Figure 1. This is a sensible compromise, if the variation in pupil sizes is not too large.

2.3 Using 4f magnifying relays

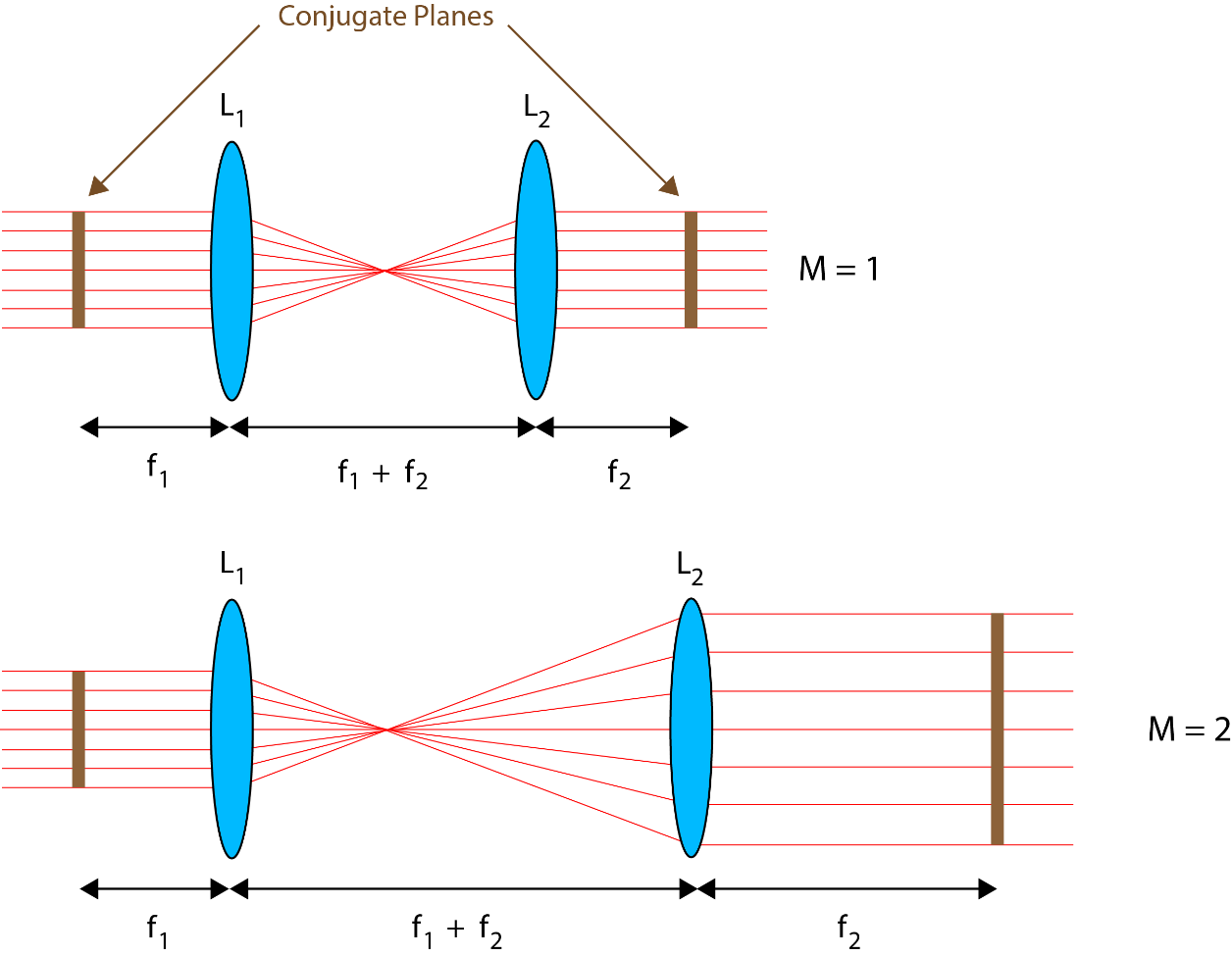
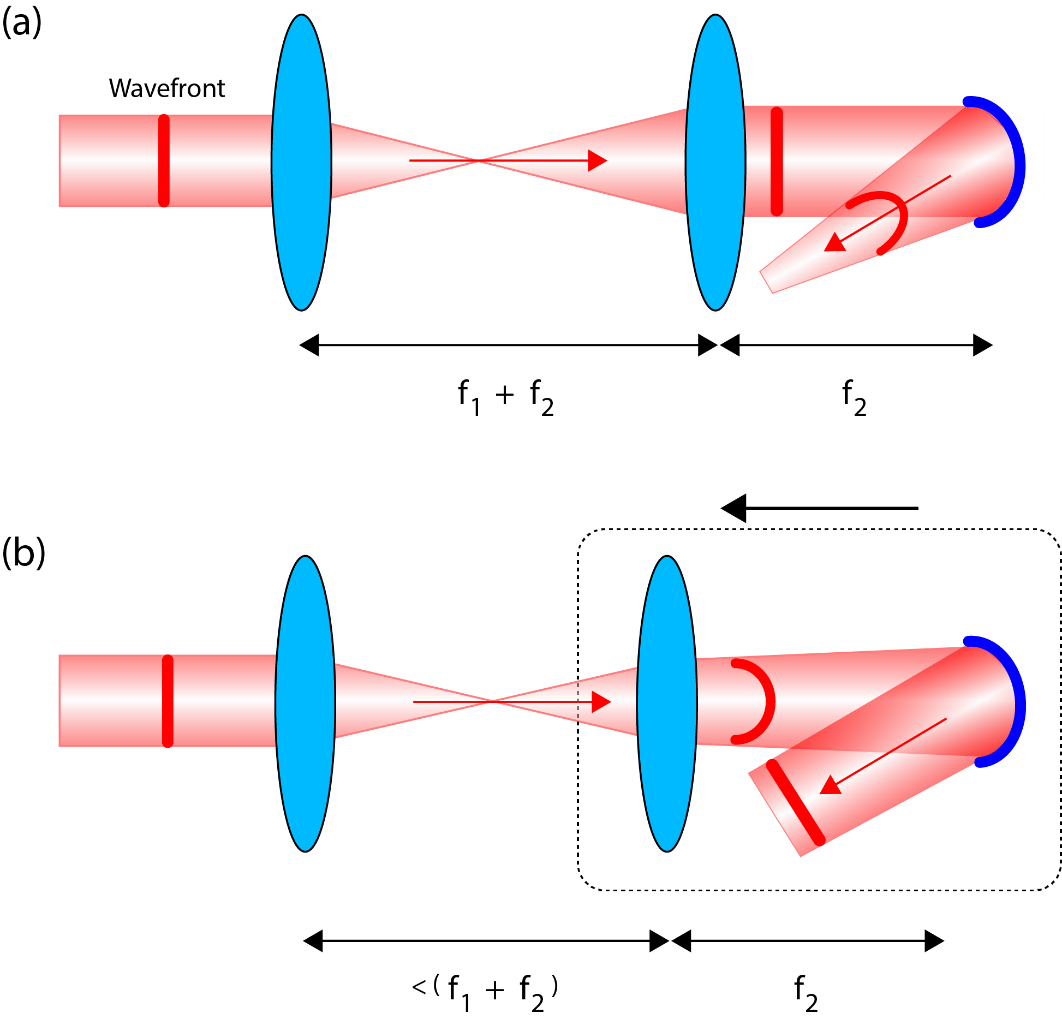
We have explained that it is essential to image pupil of adaptive element on to pupil of the objective lens. It is also important to note that this imaging step must reliably reproduce both amplitude AND phase. A single lens imaging system would, in effect, add an additional phase function that varies quadratically with radius [3]. This is avoided with the 4f imaging configuration, which can also incorporate the magnification to match pupil sizes. The magnification is obtained simply as the ratio of the focal lengths of the two lenses as illustrated in Figure 2.

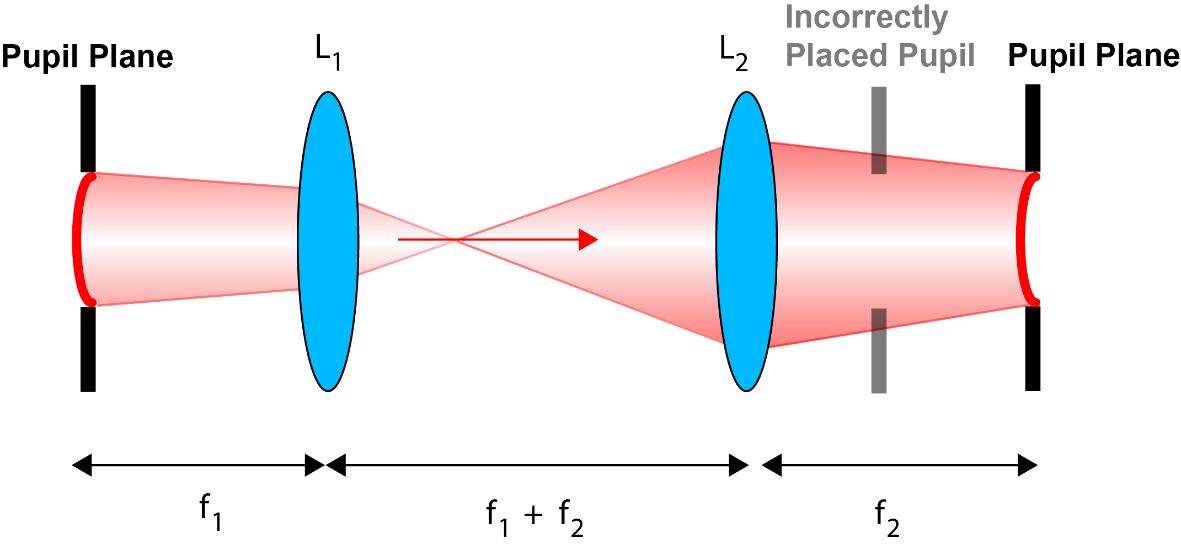
It is important to note that the correct imaging of pupil into conjugate planes is more important than collimation alone. The reason for this is illustrated in Figure 4, which shows how a misplacement of the pupil plane can lead to underfilling or vignetting when phase aberrations are present.

2.4 Angle of incidence to adaptive element

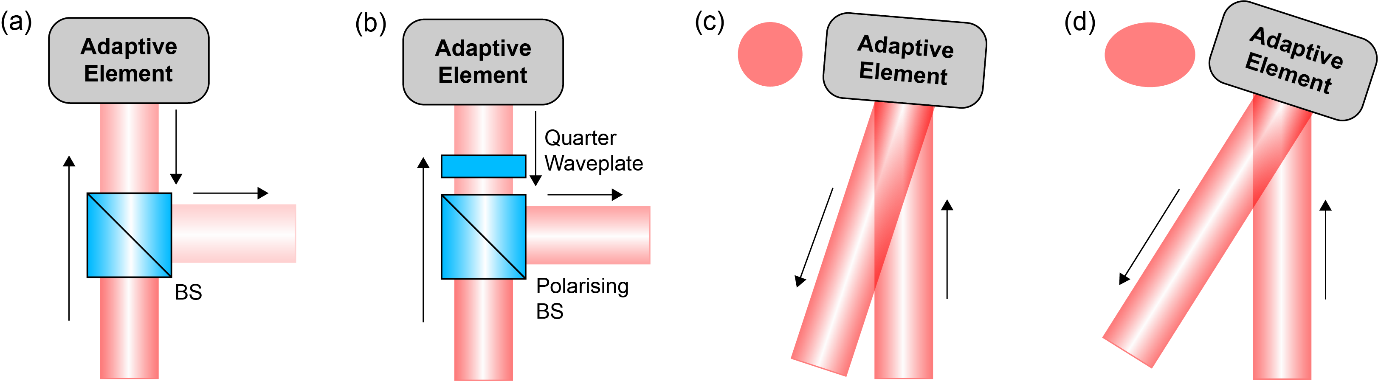
All DMs and most SLMs have to be used in a reflection configuration. They can be used at normal incidence if a beam splitter is placed before the device as shown in Figure 4(a). A polarising beam splitter can be used in conjunction with a quarter wave plate placed between the beam splitter and the AE in order to increase optical efficiency as shown in Figure 4(b). Note, however, that care must be taken when using SLMs owing to their polarisation sensitive operation [2]. A major disadvantage of this configuration is the extra reflections at the surfaces of the beam splitter.

It is usually more practical to use the AE at non-normal incidence, as there is no need for a beamsplitter or polarisation optics as shown in Figure 4(c). If the incident beam angle is at a few degrees to the normal, then the device will operate almost identically to normal incidence. While the non-normal incidence would, in theory, cause a circular beam to appear elliptical at the device, as shown in Figure 4(d), the ellipticity would be negligible and would be of no real consequence in realistic situations. Even at larger angles of incidence, the effects of the elliptical pupil could be calibrated. If important, the slight effects of path length changes due to the angle at the AE could be dealt with by a calibration step.

2.5 Single and dual pass systems

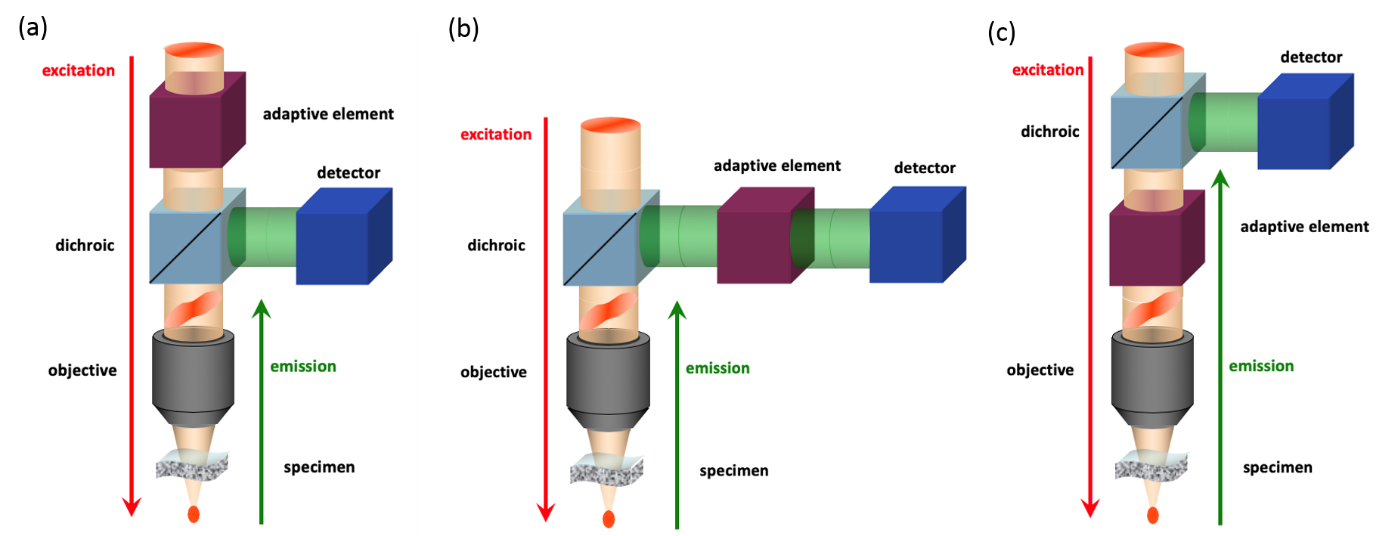
The ideal placement of AEs in the system is dependent upon the type of microscope being used. Either or both of the illumination and detection paths might need correction, dependent upon the microscope configuration. The classification of the major types of such systems can be summarised as below:

• Correction required in illumination path only: e.g. multi-photon fluorescence microscopes; other non-linear microscopes, such as second or third harmonic microscopes. This is illustrated in Figure 5(a). In these microscopes, it is typical to use a large area detector to integrate emitted light, so aberrations in the detection path have no effect on the signal. The AE can be placed only in the illumination path or in the common path.

• Correction required in the detection path only (Figure 5(b)): e.g. widefield microscopes. Typically, these microscopes use wide area illumination which is not affected by aberrations. Hence aberrations only affect the imaging path between the specimen and the camera. The AE can be placed in the detection path or in the common path.

• Correction required in both the illumination and the detection path (Figure 5(c)): e.g. optical coherence microscopy, confocal microscopy; spinning disk microscopes. In these microscopes aberrations in both paths affect image quality. Hence, the AE should be placed in the common path, or two AEs could be placed in the illumination and the detection path separately. Note that using two AEs is not commonplace owing to disadvantages such as cost.

The example microscope types mentioned above are not exclusive and several other less common methods would also fall into the same categories.

2.6 Deformable mirror active apertures

As mentioned earlier, it is desirable to use a large as possible aperture on DM in order to make best use of the available actuators. Notwithstanding this principle, it is normal practice to define the active area such that some actuators are placed just outside this area. This is necessary to be able to control the phase gradients at the edge of the pupil. This ability is essential to correct, for example, spherical aberration, which requires a rapid phase variation towards the edge. Note that some DMs have built in apertures that designed in this way already, where an outer ring of actuators are placed behind the aperture screen as shown in Figure 6.

2.7 SLM active apertures

To fully utilise the capability of an SLM, the magnification should be chosen such that the imaged pupil takes up as much of the active area as possible. As many SLMs have rectangular active areas, the diameter should be smaller than the shorter side of the rectangular active area. As it is fairly trivial to move the actively-used area on the SLM using the control software, making the pupil diameter smaller than shorter side of the pixelated area of the SLM provides flexibility in alignment.

2.8 Offsetting introduced defocus

For some DMs, it is useful to set the default position of the device to its mid-stroke position, as this permits displacements in both positive and negative directions from the default. In doing this, defocus is introduced, as shown in Figure 7(a). In order offset this defocus, both the device and the preceding lens need to be translated together as shown in Figure 7(b). The device must remain a focal length away from the lens to ensure it remains conjugate to the pupil. In practice, if the required shift is small compared to the focal length, moving only the lens will suffice.

3. Practical alignment

3.1 Mounting of adaptive optical elements

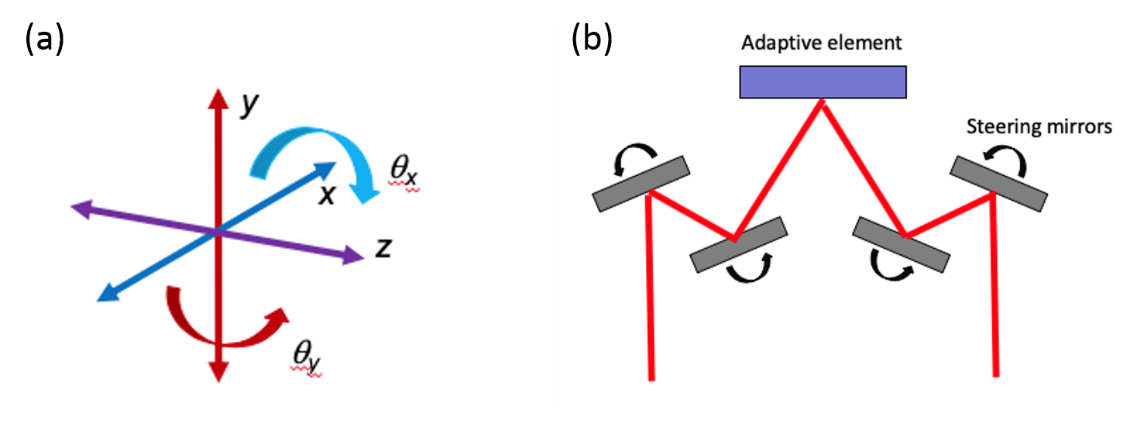
As the positioning of the adaptive element is critical, some thought should be put into its mounting. Careful design and investment in appropriate mounts can help avoid a lot of difficulties at later stages of alignment and operation. Five axis alignment, as shown in Figure 8(a), is usually required (x, y, z, θ_x, and θ_y, where z is normal to the AE surface) in order to obtain the correct pupil position on the AE and the correct relationship between beam position and angle preceding and following the device. Gimbal mounts are recommended so that tip and tilt of the device does not cause a translation. Alternatively, some of these degrees of freedom could be transferred to adjustable mirrors before and after the device as shown in Figure 8(b).

3.2 Locating and positioning system apertures

As proposed earlier, it is sensible to use the objective pupil as limiting system aperture and to align the adaptive elements relative to this limiting pupil. A common complication with this approach is that the aperture is located within the objective lens and its exact position is often unknown, as the information is not always provided by manufacturers. It is useful therefore to have experimental methods that enable the location of the aperture position.

Light passing through the objective lens from the object space through to the pupil can be used to, in effect, cast a shadow of the aperture that can be used for alignment purposes. One way of achieving this is the use of LED illumination placed below a microscope slide through a suitably diffuse scattering specimen. “Suitably diffuse” means that the light is scattered over angles greater than the acceptance angle of the objective lens, determined by its numerical aperture (NA). If the light is scattered less than this, then the pupil will not be filled and proper alignment will not be possible. A camera is positioned to image the pupil plane, so that the edge of the aperture is sharply imaged. Note that some lenses include rough edged apertures, presumably to reduce effects of light scattered/diffracted from the aperture edge. This makes location of the correct plane more difficult, but you can still look for the case where the pupil edge looks sharpest.

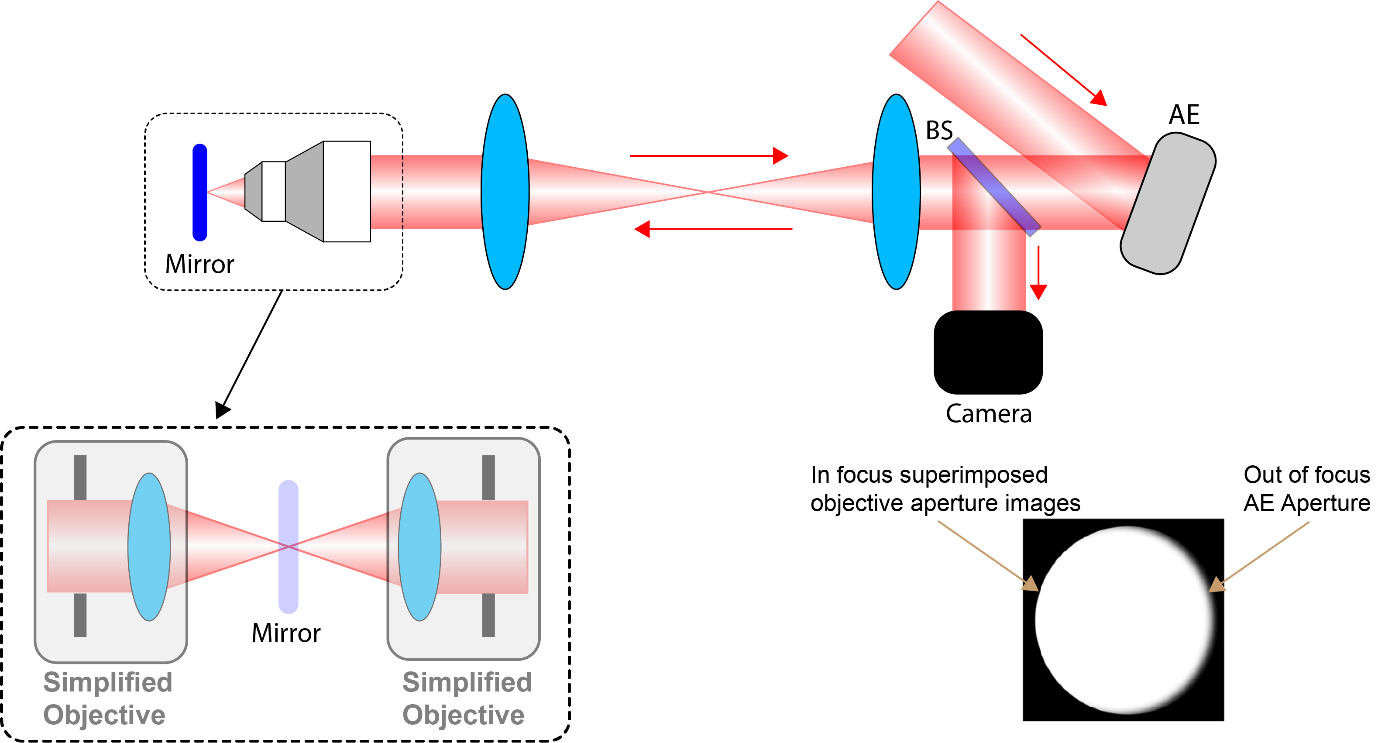
Alternatively, one can use a mirror specimen to reflect light back through the objective lens as shown in Figure 9. In this case, care needs to be taken to ensure the mirror specimen is in the correct focal plane. Assuming the 4f relay is correctly collimating the light (i.e. the two lenses are the correct distance apart), the correct placement of the mirror can be obtained by checking the collimation of the reflected beam. If the mirror is set correctly, two instances of the aperture stop of the objective will be simultaneously in focus on the camera: one from the illumination path and one from the reflection path. The reason for this is shown in the inset of the figure where the objective has been represented by a single lens and aperture. The AE can be correctly positioned by ensuring that the physical aperture of the AE (or if other alignment patterns are used – see [1,3]), is also in focus on the camera. The camera image shows an example where the aperture of the AE is slightly out of focus relative to the objective aperture owing to incorrect placement of the deformable mirror. Note that if the aperture of the DM is larger than the objective aperture, it may not be possible to view this aperture.

When incorporating an AE in a scanning system, another way to position the AE is to use one of the scanners to slowly scan the beam and place the AE at the location where the beam does not move. As the scanners are conjugate to the objective aperture, the AE will also be conjugate. This is illustrated in Figure 10.

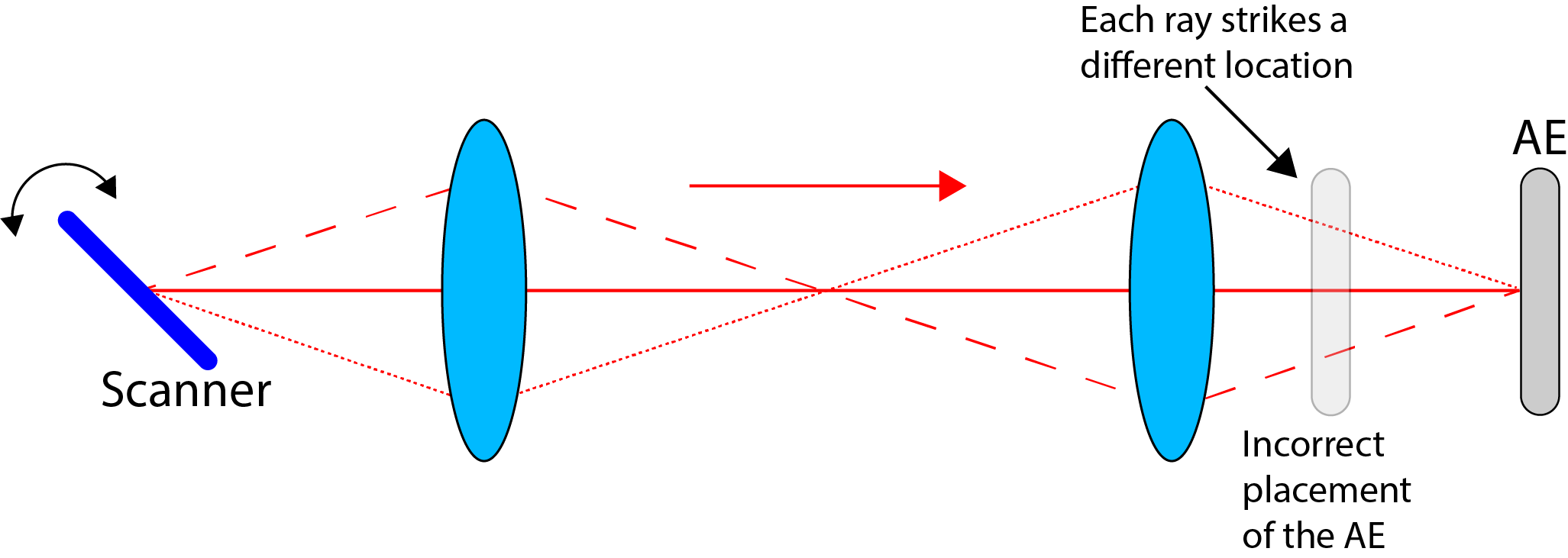
The precision of positioning required along the optical axis is dictated by the depth of focus of the 4f imaging stage leading up to the aperture or device in question. As the effective NA of these systems is small, the precision is likely to be closer to a millimetre than a micrometre. Hence, translation stages can be coarse and do not require micrometre screws.

In the vast majority of systems, the AE is inclined to the beam normal. This means that it may not be possible to get all parts of the AE into focus and a compromise position must be found. This is not generally problematic as the slight blurring involved will have little effect of the system performance. This is particularly so, as the blurring will be on a scale much less than the typical scale of variations across the AE, such as the lateral extent of the influence functions of a DM.

3.3 Alignment of deformable mirrors

Correct alignment of the AE is important to ensure that the mathematically defined phase functions are coincident correctly on the objective pupil. As explained in [1,3], step like patterns can be generated on a SLM to aid the alignment process. This is not possible on a continuous face sheet DM. Any image of the DM surface would be featureless, unless surface imperfections – or perhaps dust particles – were present. However, there are ways to reveal the position of the DM.

As mentioned above, some DMs have an aperture in front of the reflective surface and the image of this aperture can be used for lateral alignment of the DM. For some DMs, such as those from Boston Micromachines, it is possible to see structures around the active mirror surface and they can be used as a reference for both lateral and axial positioning.

Although an in-focus image of the DM would be featureless, it is possible to reveal the actuator structure by defocussing of the camera. If a phase variation is imparted across the DM, then the light propagating from the DM will exhibit intensity variations as illustrated in Figure 11. Where the wavefront has divergent curvature, the intensity decreases as the camera is moved away; where the wavefront has convergent curvature, the intensity increases. Hence, the defocused images encode the shape of the DM surface, even if the in-focus image show constant intensity. Indeed, the phenomenon can be used for quantitative calibration of a DM.

Figure 12 shows an image of an Imagine Optics DM showing uniform intensity when in focus and showing significant intensity variations when out of focus. In both cases the same control signals were applied to the DM; the four central actuators have different signals to the surrounding actuators. It is also possible to see some “print-through” where local wavefront variations are caused by the individual actuator structures. Such effects are present in most DMs and have little effect in practice on correction abilities.

Chosen test patterns can be applied to the DM in order to aid alignment. For example, drive signals applied to a central and four peripheral actuators could be used to centre the pattern of a DM on an aperture.

3.4 Flatness correction

Adaptive elements are usually not flat in their resting state – a phenomenon that arises simply as a consequence of the manufacturing processes. As such, the addition of an DM to a microscope system without any additional action to control the element will usually cause a significant decrease in performance. Clearly, the first step should be to flatten the DM using active control signals, which can be determined using, for example, a wavefront sensor, an interferometer or through optimisation (these methods are explained in other documents [4]). Manufacturers often supply a flatness calibration file when the DM is supplied. However, it is sensible to have a method to verify this flatness correction yourself, as 1) it might be wrong; 2) the necessary correction might change over time; 3) you might need to compensate additionally for other imperfections in your optical system, which mean that you need a “system” flatness correction and not just the DM flatness correction. Once this flatness correction is determined, it should be used as the default offset position before any other process is undertaken with the DM.

Figure 13 shows an example of the initial non-flat surface of a particular DM with zero control signals applied. This initial figure contains a significant amount of defocus, amongst other modes. The flattened version shows only a small amount of print-through from the actuators.

References

[1] Alignment of a SLM-based STED depletion beam, Aurélien Barbotin, https://aomicroscopy.org/sted-alignment.

[2] https://www.microscopyu.com/microscopy-basics/infinity-optical-systems.

[3] Designing and aligning optical systems incorporating liquid crystal spatial light modulators (SLMs), Patrick Salter and Martin Booth, https://aomicroscopy.org/slm-alignment.

[4] Calibration and Closed-Loop Control of Deformable Mirrors Using Direct Sensing, Karen Hampson and Martin Booth, https://aomicroscopy.org/dm-calibration-direct-sensing.