Sensorless Adaptive Optics
For citeable PDF versions of this document, please use the links below.
- DOI (concept): https://doi.org/10.5281/zenodo.4065529
- DOI (version): https://doi.org/10.5281/zenodo.4066425
- Authors: Karen Hampson, Jacopo Antonello, Richard Lane, Martin Booth
- Last modified: 5 yrs ago
The listed authors have participated in the writing of this document. As the content is the culmination of long term work in the Dynamic Optics and Photonics Group, many others have contributed directly or indirectly to this material. We consciously acknowledge all of these contributions, even though it is impractical to list them all here
1. Introduction
Wavefront-sensorless adaptive optics (AO) is widely used for aberration correction in microscopes. The original AO systems consisted of an adaptive element, such as a deformable mirror, that could correct aberrations and a wavefront sensor for aberration measurement. However, many methods have been developed that do not require the sensor. These are wavefront-sensorless AO systems. Frequently, as a short-hand, the word "sensorless" is used for "wavefront-sensorless". In a sensorless AO system the aberrations are inferred from a sequence of image measurements taken with changes applied to the adaptive element - a wavefront shaping device used for aberration correction. The technique is also sometimes referred to as indirect wavefront sensing as, despite the lack of a wavefront sensor, the aberrations can still be quantified. Fundamentally, sensorless AO involves the optimisation of image quality, while varying the settings of the adaptive element; the assessment of image quality is used to inform the changes in the adaptive element.
A simple analogy to sensorless AO is the case of manually focussing a microscope objective as shown in Figure 1. The position of the objective is adjusted while one monitors the image quality. The optimum position is found when the image quality is maximised, e.g. when it has the highest contrast. While in this case the only variable is focal position (or the defocus aberration), the concept can be extended to more complex aberrations.

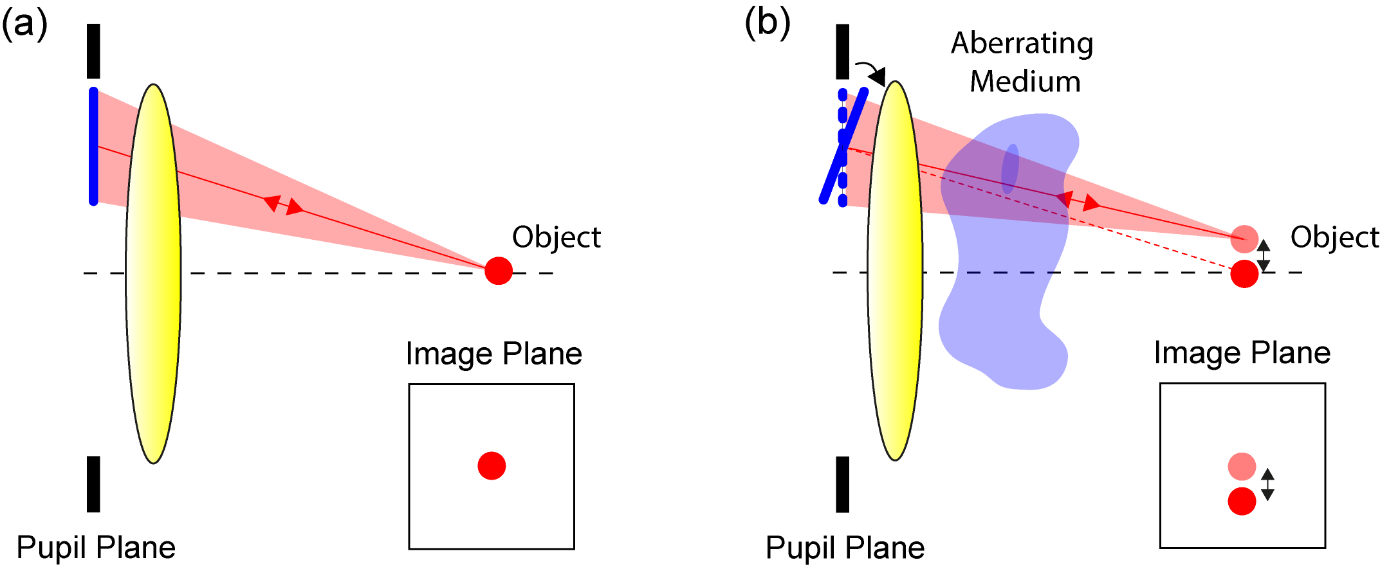
There are numerous advantages of using sensorless AO. It requires no extra hardware, other than an adaptive element and associated optics, and so is low cost in comparison to systems that employ a wavefront sensor. There are also no non-common path errors, the origin of which is shown in Figure 2. Also, all of the available light can be used for imaging as there is no need to send some of this light to the sensor using a beamsplitter. There might also be cases where the signal level is too low for direct wavefront sensing. A further advantage of sensorless AO is that it can be used in situations where sensing may not be possible owing to the nature of the light returning from the sample. For example, the Shack-Hartmann sensor [1], which is the most common wavefront sensor, requires that the light used for sensing is confined to a small region as shown in Figure 3. This is not possible in wide-field fluorescence imaging systems, if the fluorescence is distributed throughout a volume of the specimen. Although the Shack-Hartmann can be used in two-photon imaging, it may be difficult when imaging deep into the specimen.
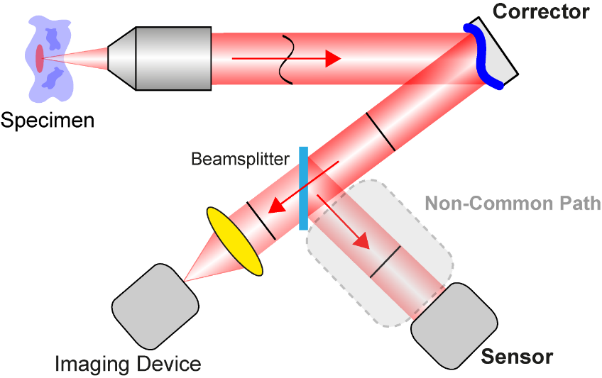
The main disadvantage of sensorless AO is speed, as it requires a sequence of images to measure and correct a given set of aberration modes. On the contrary, direct wavefront sensing methods, such as Shack-Hartmann wavefront sensing, are able to obtain the set of aberration modes in parallel, using a single measurement. Although in microscopy the aberrations are typically static at a given imaging position, extended imaging times may lead to photobleaching through over-exposure. Specimen movement during the measurement sequence, either through live specimen motion or through mechanical drift, could also cause problems.
When implementing sensorless AO, it is difficult for a newcomer to the field to know which specific implementation to choose for their particular situation. The goal of this tutorial is to address this choice by discussing the merits of approaches to the three main components of sensorless AO:
1) Method to change the correction applied (e.g. by manipulating modal aberrations).
2) Selection of an image-quality metric.
3) A procedure (algorithm) to obtain the required corrector setting from the measurements.
Using the example of manually refocussing the objective, the method of changing the correction would be modal as the magnitude of defocus is being adjusted. The image quality metric would be contrast. The procedure would be to adjust the objective position in one direction, and if this initial adjustment is in the direction of increasing contrast, the adjustment would continue in that direction until a position is found just before the image gets worse. Then the objective direction would be reversed until the focus setting results in the best image quality.
Note that, even though sensorless AO does not use a wavefront sensor, the corrector requires calibration before use. The reader is referred to our other tutorials for information on this topic [1,2].
2. Correction method
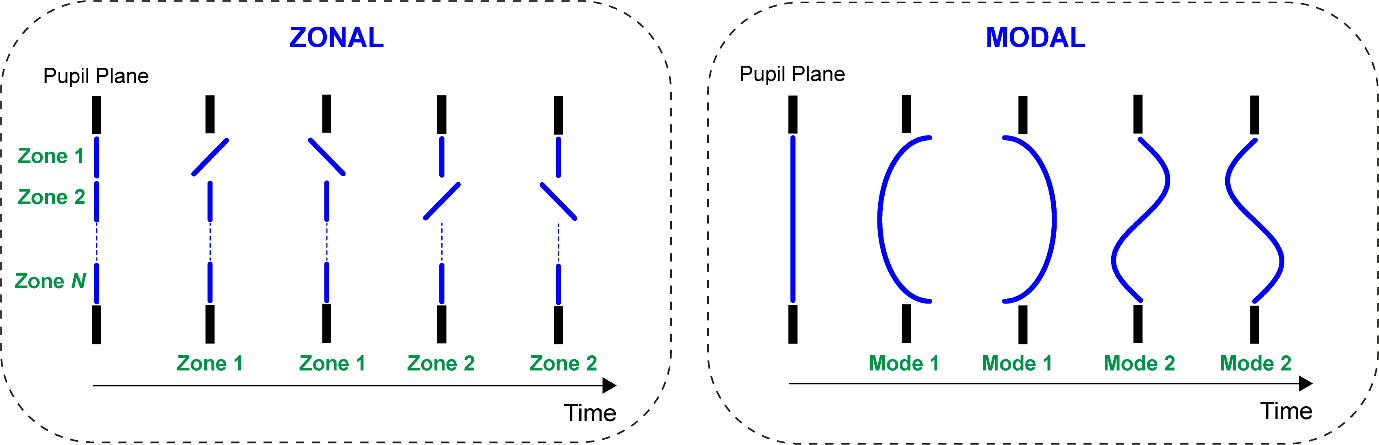
There are a range of implementations of sensorless AO. Two common categories can be termed zonal and modal. Both methods are illustrated in Figure 4. In the zonal case, the pupil is considered to consist of segments that are individually controlled. Zonal techniques are typically carried out using phase-only liquid crystal spatial light modulators (LC-SLMs) or segmented deformable mirrors. Piston-only or piston, tip and tilt are modulated, depending on the corrector. In the modal case, the wavefront shape across the entire pupil is changed sequentially. Consequently, this method is more suitable for continuous surface correctors such as continuous surface deformable mirrors. Each mode could be a Zernike polynomial, for example. In all cases, images are acquired while different settings are applied to the adaptive element. For a discussion of hybrid techniques where aberrations beyond tip, tilt and piston are applied to individual zones, see [3].
2.1 zonal method for piston-only correctors
For piston-only correctors, such as piston-only segmented deformable mirrors or LC-SLMs, the piston of each segment (refractive index of each pixel in the case of a LC-SLM) is adjusted to obtain the maximum intensity at the image plane. This amounts to the rays being in phase as shown in Figure 5 [4].
2.2 Zonal method for piston-tip-tilt correctors
Figure 6 describes the principle of the zonal technique referred to as pupil segmentation [5]. Each zone in the pupil is illuminated sequentially and the shift in the image is measured. These image shifts are caused by the local tip/tilt induced in the wavefront segment by the refractive index structure of the specimen. From these measurements, the slope of the wavefront in each zone is determined, much like the Shack-Hartmann sensor. Consequently, the mirror's segments can be set to the correct tilt. Note that modulation of the angle of the rays ensures that they meet in the correct position at the image plane, but does not guarantee they have the same phase. In order to do this, the piston of each segment is adjusted to ensure constructive interference. This step of piston correction is similar in principle to that employed in the previous section (as shown in Figure 5).
2.3 modal correction
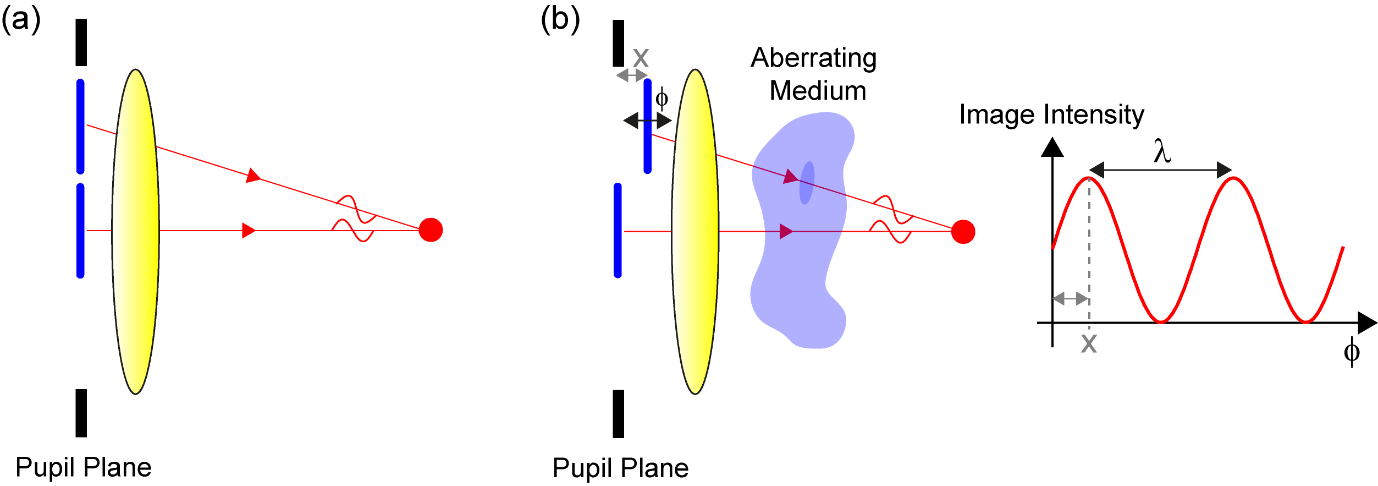
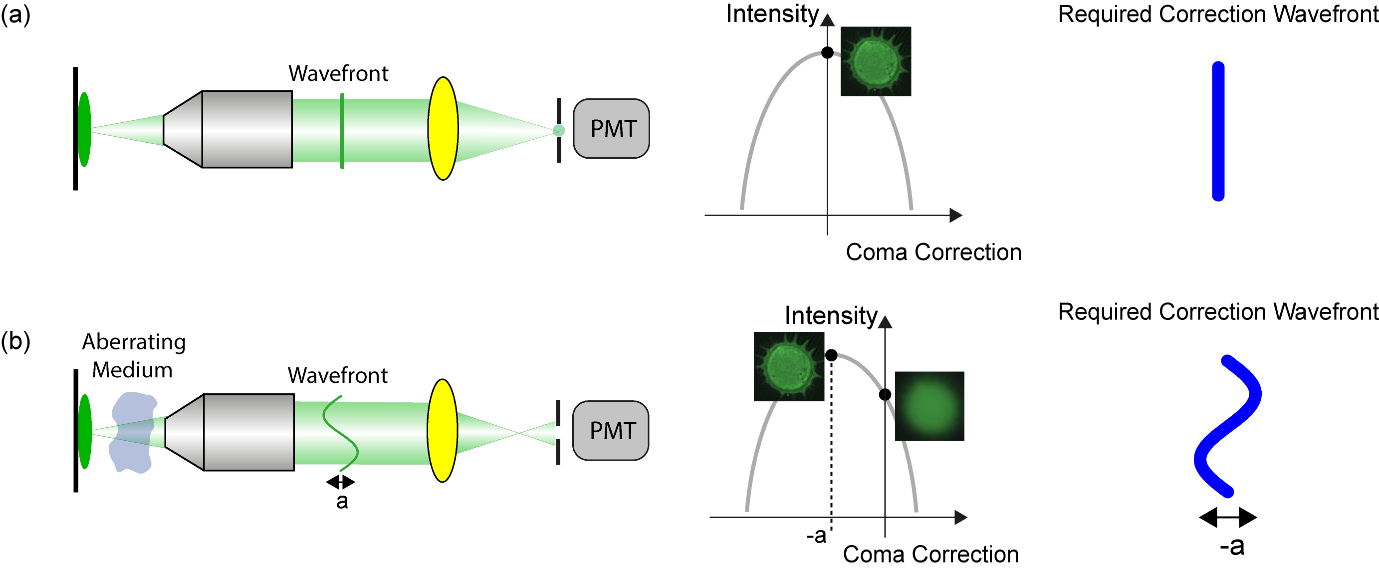
Figure 7 shows the simple example of correcting the mode coma with an adaptive element in a confocal microscope. If there are no aberrations, the metric curve will have a peak intensity when the adaptive element is planar as shown in Figure 7(a). If there is coma present, owing to an aberrating medium, the peak intensity of the curve will be shifted as shown in Figure 7(b). By measuring how the intensity varies with the magnitude of coma applied to the corrective element, it is possible to determine the optimum amount of coma to correct for the coma introduced by the aberrating medium. This can be repeated for any other aberration modes present. This article will now focus on modal sensorless AO.
3. selecting an optimisation metric
3.1 types of metric
The optimisation metric needs to be chosen appropriately for the type of microscope in order to ensure that it exhibits a clearly defined maximum (or minimum) when the aberration is corrected. A metric suitable for one form of microscopy is not necessarily useful for another. One of the simplest metrics is brightness or total image intensity (calculated as the sum of all image pixel values). This is commonly used, for example, in adaptive optics confocal or multi-photon microscopes [6]. The brightness of the image in a confocal microscope depends on how much light can pass to the detector. Aberrations decrease the maximum value of the PSF, so less light passes through the pinhole. By reducing the aberrations, the peak intensity of the PSF increases, and so more light is able to get through the pinhole. Thus, it can be seen that image intensity is an appropriate metric that is sensitive to aberrations. The same metric can also be used in two-photon systems as focal fluorescence emission is proportional to the square of the focal intensity [7].
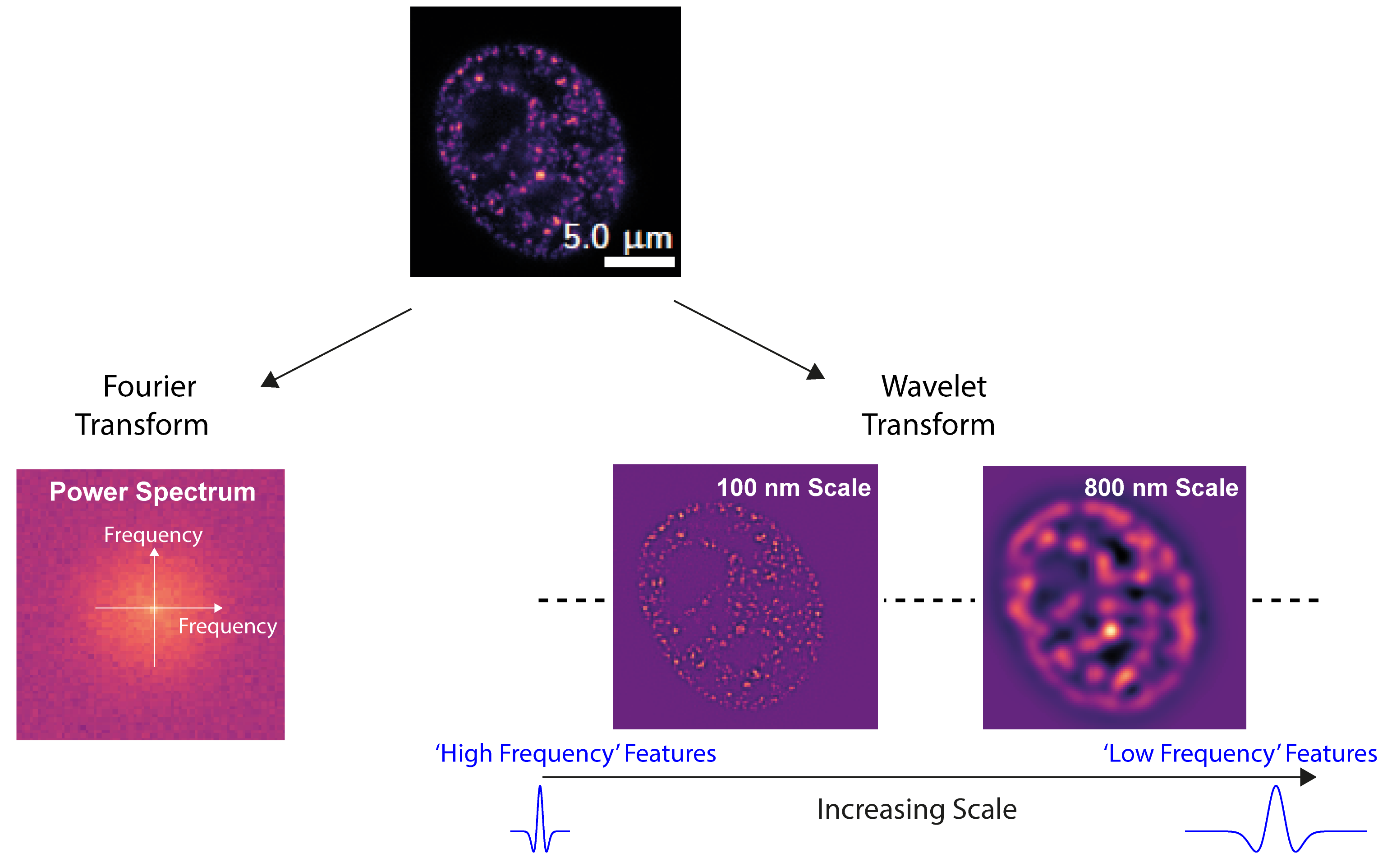
The total intensity metric is not suitable for all microscopies. For example, in a wide-field microscope, the total intensity does not change with aberrations, although the image quality does decrease. Another common metric, which is suitable in this case, is image sharpness. This is often calculated by analysing the amplitudes of the frequency content of an image using the Fourier Transform (FT) [8]. It has been implemented in a wide variety of microscopes such as wide-field and structured illumination microscopes [9]. Using structured illumination to generate additional high frequency content in the image of sparse samples has been shown to improve the reliability of sensorless AO using the FT [9], i.e. it is more likely to converge to the correct aberration correction.
The high spatial frequency information in a sample often occurs at limited locations in the image, corresponding to the fine structures of the specimen, as shown in Figure 8 for a HeLa cell. The traditional implementation of the FT however, assumes each frequency spans the entire domain of the signal, i.e. the full area of the image. A solution is to use the wavelet transform in which frequency information is localised. Rather than using sine and cosine waves that span the entirety of the image, spatially limited wavelets of various scale (analogous to the inverse of the spatial frequency), are used as shown in Figure 8. Wavelet analysis has been demonstrated to be a broadly applicable method for sensorless AO [10].
3.2 properties of a metric
An ideal metric should exhibit a global extremum where the residual aberration is zero (or strictly speaking has constant phase) with no local extrema nearby. Ideally the metric should resemble a unimodal smooth function for a range of aberrations that encompass the magnitude of the aberrations you expect to find. In practice, the range of aberration magnitudes over which the aforementioned properties hold may be limited. In certain scenarios, it has been shown that the metric definition can be tweaked in order to vary the range of operation [10].
3.3 operations with volume specimens
There is often a concern about whether such optimisation could introduce artefacts when imaging specimens with three dimensional structure. One commonly mentioned scenario is a potential problem that could occur when maximising the total intensity. For example, when imaging above or below a bright object, maximising the total intensity may lead to an increase in the aberration or a change in the focus position. However, if the system is set up so that defocus cannot be introduced by the adaptive element, then it will not be possible to inadvertently shift the imaged plane.
4. selecting an algorithm
4.1 model-based versus model-free algorithms
The algorithms can broadly be categorised as model-based and model-free. For most practical scenarios in microscope imaging, there is a well-defined mathematical model of the image formation process, including the effects of aberrations. This provides a wealth of information that can be used to inform the effects of aberrations, which can be exploited in the aberration correction procedure.
In a model-based strategy, the model provides prior knowledge of the metric function and its variation with aberrations. Often, this function can be approximated near the maximum by a parabola as depicted in Figure 1, which shows the variation of image contrast versus location of the objective. As a result, the aberration correction problem is cast into the problem of fitting a parabola through a number of data points and subsequently finding its extremum. This procedure entails taking at least the minimal number of measurements necessary to resolve all the parameters (e.g. magnitude of different aberrations) in the function used as the model for the image quality metric. This is much faster than model-free methods, which typically require many more measurements. Consequently model-based aberration correction can be applied with minimal exposure of the specimen. Owing to the advantages of speed or the minimisation of specimen exposure, the remaining focus of the article will be on model-based algorithms.
For readers interested in stochastic algorithms, example are: stochastic parallel gradient descent, genetic algorithms, and Nelder-Mead. The choice of stochastic algorithm may affect significantly the number of measurements required, although they should all reach similar solutions. When the imaging model is well understood, these model-free methods may not be the most appropriate choice. In situations where there are significant unknowns in the imaging model, a model-free approach might be appropriate. Similarly, they may be useful in cases where an improved, but only non-optimal correction can be obtained.
4.2 specifying model-based schemes
4.2.1 selecting a basis set for aberration representation
We need to represent mathematically a basis set of aberration modes, which are in essence the shapes applied to the corrector. A number of different basis sets have been used to represent the aberrations, including Zernike polynomials, Legendre polynomials, Fourier modes, Lukosz modes, and Walsh-Hadamard modes. These reasons are:
1) The modes may be optimal for a particular correction scheme, as they each have an independent effect on the image quality metric. This requires fewer measurements (see Section 4.3.1.)
2) They may be ideally correlated with the aberrations present.
3) They are well matched to the correction device, such as mirror deformation modes. Mirror deformation modes are orthogonal shapes that the mirror can produce [2].
4) They may be mathematically convenient. For example, Zernike aberration polynomials are orthogonal over a circular aperture and some low order modes represent common physical phenomena, such as image shifts (tip/tilt/defocus) or spherical aberration (e.g. from imperfect lenses).
Frequently, Zernike polynomials are chosen, even though they may not be optimal, as they can usually only be approximated by the wavefront shaping device. This choice is rarely ideal, but is a convenient starting point that many people choose, as the modes represent common optical phenomena, such as defocus, astigmatism or spherical aberration. Consequently, the remainder of this section will focus on practical implementation with Zernike polynomials. The first few Zernike polynomials, up to and including 4th radial order are shown in Figure 9. There are slight variations in the way in which Zernike polynomials are defined. In particular, different normalisations can be used. Zernike's original definition was normalised such that the radial component of the function was 1 at a radius of 1. In microscopy, we have found it more useful to use the normalisation where the root-mean-square value of the mode is normalised to 1. For the common optimisation metrics, based upon total intensity, we find that using this normalisation the same amount of each mode gives a similar effect on the metric. Hence, we usually use the normalisation and ordering of the Zernike polynomials defined by Noll [11]. Note that the OSA ANSI standard uses the same normalisation as Noll's, although the ordering and numbering of the modes are different, for example.
4.2.2 correcting a single mode
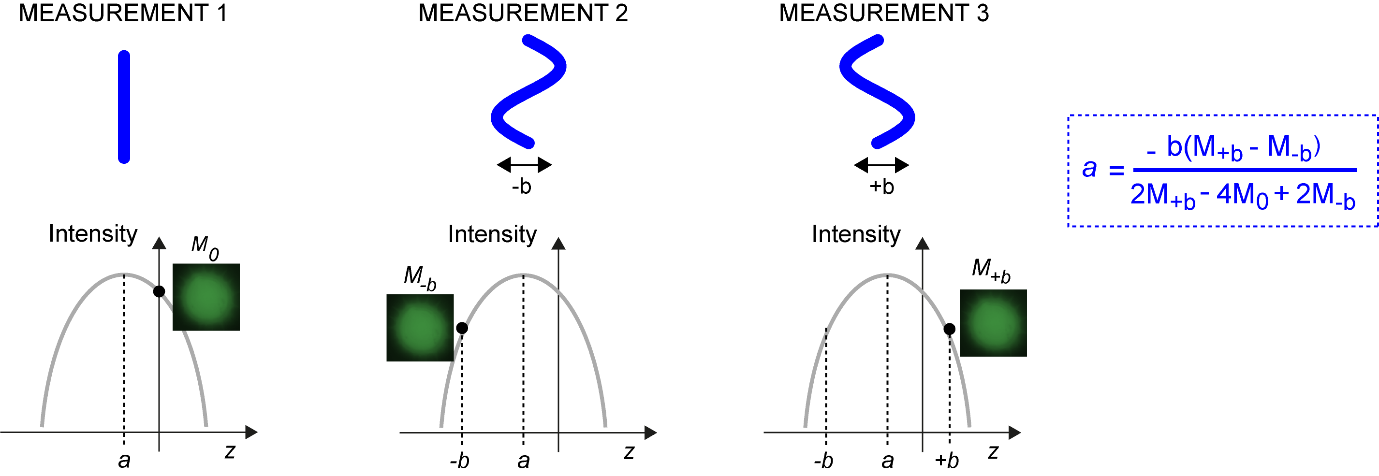
Recall Figure 7 which shows the simple example of correcting coma with an adaptive element in a confocal microscope. If coma is introduced by an aberrating medium, the peak of the intensity metric will occur when the coma applied by the corrector has an equal but opposite magnitude to that introduced by the aberrating medium. The goal is to determine this value. This can be achieved by applying a series of different corrections for coma while recording the corresponding value of the metric at each step. One can subsequently fit a function through the measured values of the metric and obtain the optimal coma correction as the value that maximises the fitted function. Since one knows a priori that the fitted function is approximately parabolic in shape, one can choose a parabola for the fit function, thus minimising the number of free parameters that need to be estimated and consequently the number of images that must be recorded. The required correction can be determined from three intensity measurements as shown in Figure 10. These measurements are: one with the corrector introducing no wavefront, and one each with the coma introduced by the adaptive having a magnitude of -b and +b, referred to as bias measurements. The required correction can be determined from the equation shown in the Figure 10.
4.2.3 extending to n modes
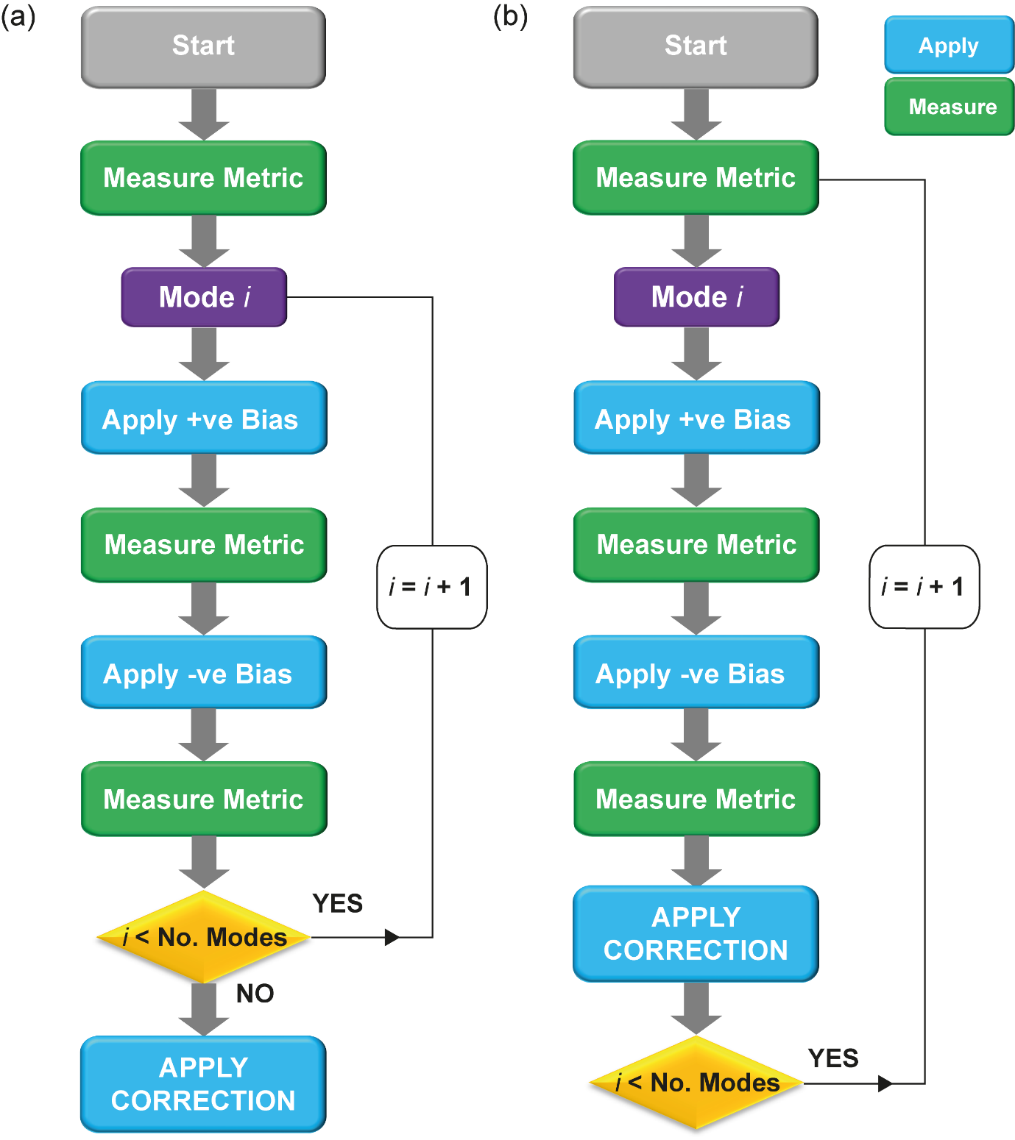
There are two main ways in which the measurement and correction is carried out when correcting multiple modes. These are summarised in Figure 11. In the first method, as shown in Figure 11(a), all modes are measured first, with the correction applied to the corrector at the end. This is referred to as the 2N + 1 algorithm, as there are two measurements per mode (for biases of +b and -b) plus one measurement when no aberrations are applied [12]. In the second method, as shown in Figure 11(b), the correction of each mode is applied sequentially, again with two measurements per mode (for biases of +b and -b) plus one measurement when no aberrations are applied. In this case, a new ‘zero bias’ measurement would be required after each aberration measurement and correction. Consequently, 3N measurements would be required. When aberrations are large, the 3N algorithm is more appropriate [12]. The benefit of correction is obtained sooner, as updates are implemented sequentially rather than simultaneously, but requires more measurements overall. In practice, in both cases, to improve robustness in low signal-to-noise situations, more than the minimum number of 2N + 1 or 3N measurements, is often required. Note that the formula to calculate the correction for each mode in Figure 10 is pertinent to fitting the parabola for each mode with three points. In general, more sophisticated fitting algorithms can be used.
4.3 practical implementation of model-based algorithms using zernikes
4.3.1 Number of measurements
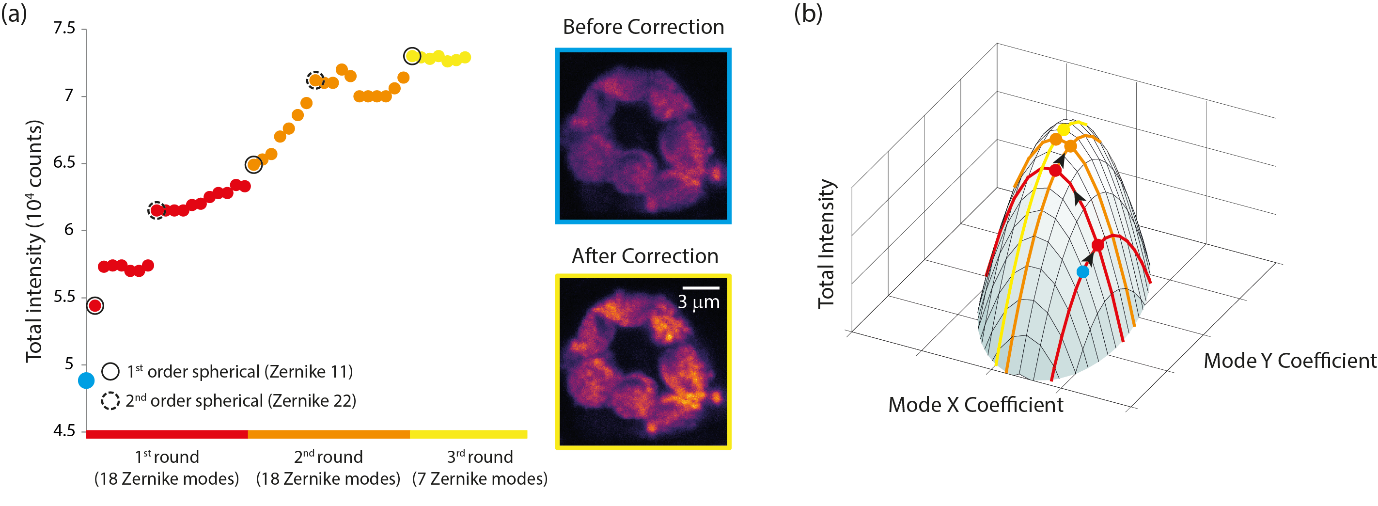
The two aspects concerning the total number of images required to apply the correction (equal to the number of metric measurements), are the number of measurements per aberration mode, and the number of times the sensorless AO algorithm is repeatedly applied. The number of measurements per aberration mode primarily depends on the signal to noise ratio and the magnitude of the aberrations. For aberrations smaller than 0.5 rad rms, one iteration of the 2N + 1 algorithm is expected to remove most of the aberration. For amplitudes between 0.5 and 1 rad rms, the 5N can offer a more robust performance. Figure 12 shows an example of correcting a specimen in which multiple aberrations are present. Note that several correction cycles (or rounds) are required to reach the optimum correction. Although Zernike aberration modes (and other basis sets) are orthogonal in the pupil plane, it does not necessarily mean that each has an independent effect on the image quality metric. This is referred to as modal cross-talk or coupling. Other ways to mitigate this are found at [13]. This lack of independence is illustrated in Figure 12(b) by the paraboloid not being perfectly aligned to the axes. Other potential causes are that the corrective element doesn't perfectly recreate Zernike modes, the parabolic fitting is not precise, or because the initial aberration is too large for the small aberration approximation on which the paraboloidal model is based.
4.3.2 Number of modes to use
The choice of the number of modes depends on capabilities of the corrector and prior knowledge about the aberrations in the specimen. A few low-order modes (10 to 15) typically suffice if focussing tens of micrometres into transparent specimens, whereas a large number are required for strongly scattering specimens. Note that piston, tip, tilt and defocus should not be used. This is because piston, tip and tilt, do not affect image quality, although tip and tilt will cause an image shift. The effect of defocus is equivalent to translating the specimen and objective relative to each other along the axis, which is also an image shift for three-dimensional imaging. If aberrations exist in the specimen that the corrector cannot compensate, owing to spatial resolution or dynamic range, there is no point in trying to correct them. The choice of which modes to correct may also vary depending on the type of microscope, e.g. the sensitivity to certain modes is enhanced in structured illumination microscopy, if the modes affect the structured patterns.
4.3.3 Order of mode correction
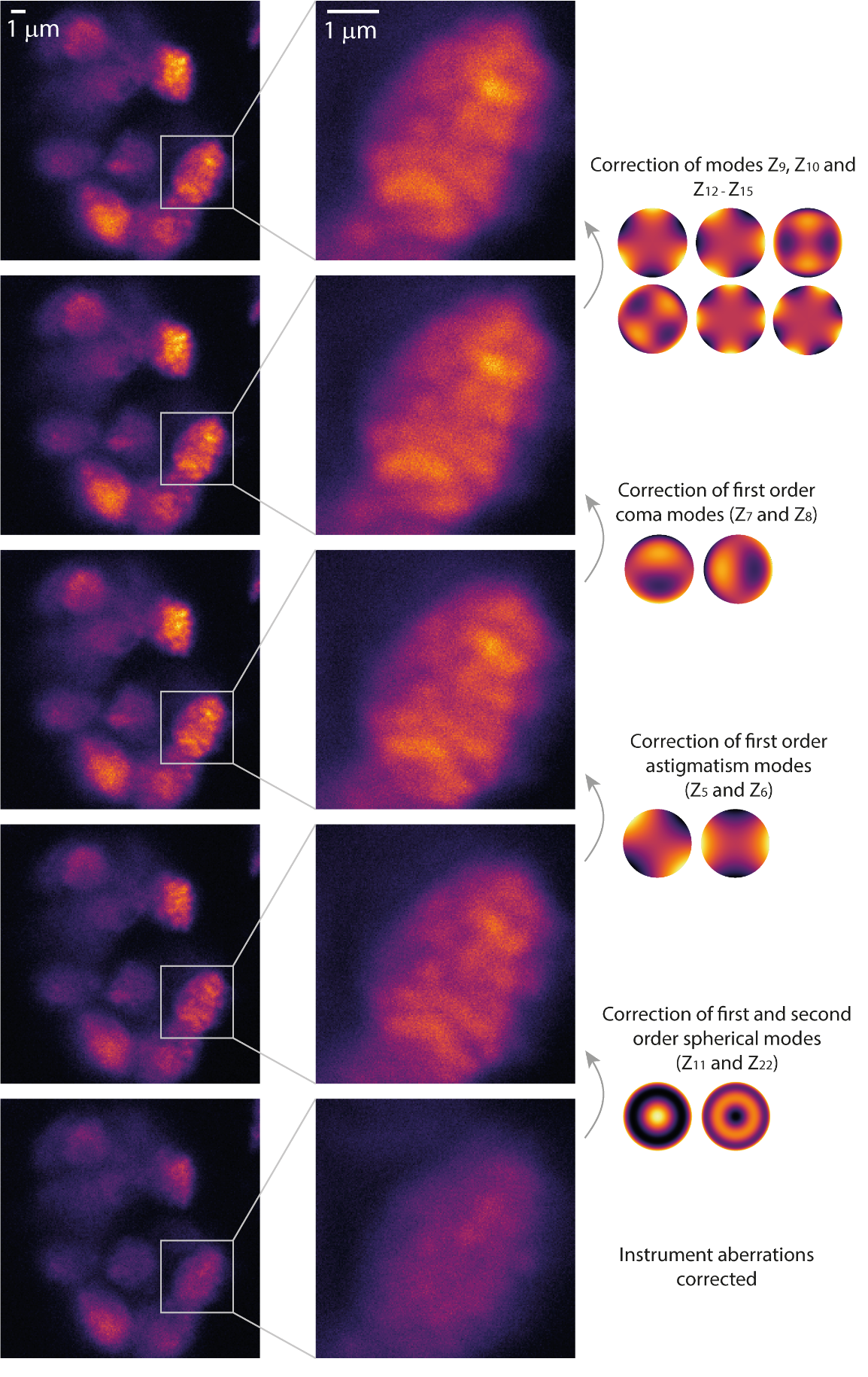
Taking simply the first N modes in the list is not necessarily the best strategy. If you have one particularly large aberration, e.g. such as spherical aberration due to a large refractive index mismatch, that should be corrected first. The correction of subsequent modes will then be more effective. Note that correction of Zernike spherical aberration may cause refocussing. Figure 13 shows an example of image improvement with correcting various aberrations not in the order they appear in the Zernike triangle as shown in Figure 9.
4.3.4 magnitude of bias aberration introduced by the corrector
The effective implementation of these sensorless AO methods requires a sensible choice of the size of the bias aberrations introduced by the corrector. As a rule of thumb, these bias magnitudes should be in the region of the half-width-half-maximum (HWHM) of the response curve of the metric. As this may not be known in advance, it can be estimated through a calibration step when setting up the system. This is implemented by measuring the metric for each aberration for a range of coefficients introduced by the adaptive element. From the resulting curves, it is possible to estimate the HWHM and choose a bias magnitude similar to this. During this process it is important to consider limits of corrective device, so that the device does not saturate. The maximum Zernike coefficient that can be generated for each aberration is limited by the physical properties of the device.
5. conclusion
In this article, we have outlined the principles of sensorless AO and explained the modal implementation in more detail. Using the image quality itself to drive the aberration correction, without using a wavefront sensor, has numerous advantages over sensor-based correction, such as having a lower cost and not requiring extra hardware for a dedicated wavefront sensor. It can also be applied in scenarios where traditional sensor-based methods cannot. The choice of sensorless method will be influenced by the nature of aberrations in the specimen and the choice of adaptive element. In the modal approach, the required correction is obtained by fitting the data from a sequence of image measurements with applied aberrations. Although not necessarily ideal, the Zernike modes are often a good starting point. We have outlined how to specify such an approach to sensorless AO and provided guidelines on various implementations. Further specific details are available in the primary literature referenced in this article.
References
1) K. M. Hampson and M. Booth, "Calibration and closed-loop control of deformable mirrors using direct sensing," https://aomicroscopy.org/dm-calibration-direct-sensing
2) J. Antonello, J. Wang, C. He, M. Phillips, M. Booth, "Interferometric calibration of a deformable mirror," https://aomicroscopy.org/dm-calib
3) Q. He et al., "A universal framework for microscope sensorless adaptive optics: generalized aberration representations," APL Photonics 5, 100801 (2020).
4) R. Lui, D. E. Milkie, A. Kirlin, B. Maclennan and N. Ji, "Direct phase measurement in zonal wavefront reconstruction using multidither coherent optical adaptive technique,"Optics Express 22, 1620-1628 (2014).
5) D. Milkie, E. Betzig and N. Ji, "Pupil-segmentation-based adaptive optical microscopy with full-pupil illumination," Optics Letters 36, 4206-4208 (2011).
6) M. J. Booth, M. A. A. Neil, and T. Wilson, "New modal wave-front sensor: application to adaptive confocal fluorescence microscopy and two-photon excitation fluorescence microscopy," J. Opt. Soc. Am. A 19, 2112-2120 (2002).
7) M. J. Booth, "Adaptive optical microscopy: the ongoing quest for a perfect image," Light: Science Applications 3, e165 (2014).
8) D. Débarre, M. J. Booth and T Wilson "Image based adaptive optics through optimisation of low spatial frequencies," Optics Express 13, 8176-8190 (2007).
9) M. Žurauskas et al., "IsoSense: frequency enhanced sensorless adaptive optics through structured illumination," Optica 6, 370-379 (2019).
10) J. Antonello, A. Barbotin, E. Chong, J. Rittscher and M. J. Booth, “Multi-scale sensorless adaptive optics: application to stimulated emission depletion microscopy,” Optics Express 28, 16749-16763 (2020).
11) R. J. Noll, “Zernike polynomials and atmospheric turbulence,” JOSA 66, 207-211 (1976).
12) A. Facomprez, E. Beaurepaire, and D. Débarre “Accuracy of correction in modal sensorless adaptive optics,” Optics Express 20, 2598-2612 (2012).
13) M. J. Booth and M. Jesacher, “Sensorless Adaptive Optics for Microscopy,” In: Adaptive Optics for Biological Imaging, Ed. J. Kubby, CRC Press (2013).
Return to documents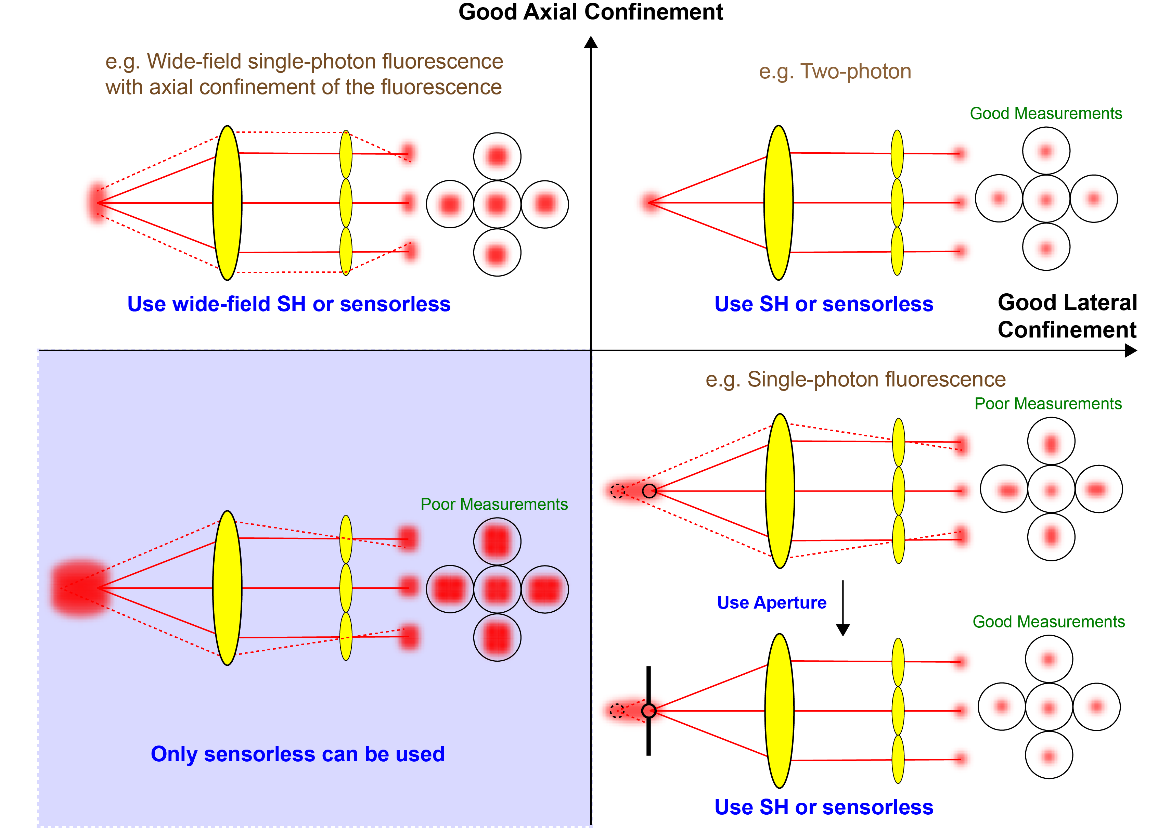
![Figure 9. Zernike basis set up to and including 4<sup>th</sup> radial order using the Noll convention \[11\]. The radial order describes the highest power of the component that varies across the pupil. For example, for defocus, which has a radial order of two, the variation across the pupil is described by a quadratic. The azimuthal frequency denotes the number of peaks and troughs as the angle θ varies. Negative numbers correspond to a sinusoidal variation, equivalent to sin(-mθ), whereas positive numbers represent a cosinudoidal variation. For example, for oblique astigmatism, which has an azimuthal frequency of -2, there are two peaks and troughs with a sinusoidal phase. Note that in the box labelled “meaning of radial order”, the expressions represent the highest order polynomial terms present and not the exact mathematical form.](/user/pages/01.home/12.Sensorless-AO/media/image10.png)